题目内容
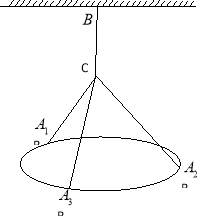
【题目】一吊灯下沿圆环直径为
米，通过拉链
、
、
、
（
、
、
是圆上三等份点）悬挂在
处，圆环呈水平状态并距天花板2米，如图所示.
（1）为使拉链总长最短，应多长？
（2）为美观与安全，在圆环上设置，，……，
（
）各等分点，仍按上面方法连接．若还要求拉链总长度最短，对比（1）时C点位置，此时C点将会上移还是会下移?请说明理由.
【答案】（1）
；（2）
点的位置将下移.
【解析】
试题分析：（1）设
离天花板
米（
），拉链总长度为
米,利用所给图,得到
,其导,利用导数求出
取何值时,
最小；（2）当在圆环上设置
个点时,拉链的总长为
,同样利用导数求出
取何值时,
最小.并与（1）中值比较,可知
点的位置移动情况.
试题解析：
（1）设离天花板米（），拉链总长度为米，由题意
、
、
、
四点构成一个正三棱锥，
、
、
为该三棱锥的三条棱侧，三棱锥的高
.于是有，对其求导，得
.
当
时，
，解得
时，
，
时，
，
时，即米时，
取最小值
米.
（2）由（1）可知，当在圆环上设置
个点时，拉链的总长为：，求导得
，当时，
.解之得
，因为
只有一个极值，所以时，拉链长最短.下面比较
与
的大小
（其中
），即
，亦即得
，所以点的位置将下移.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
