题目内容
如图,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5AA1=4,点D是AB的中点.
(1)求证:AC⊥BC1;
(2)求多面体ADC-A1B1C1的体积;
(3)求二面角D-CB1-B的平面角的正切值.

(1)求证:AC⊥BC1;
(2)求多面体ADC-A1B1C1的体积;
(3)求二面角D-CB1-B的平面角的正切值.

(1)证明:直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4,AB=5,
∵AC2+BC2=AB2
∴AC⊥BC,
又AC⊥C1C,C1C∩BC=C
∴AC⊥平面BCC1;
∴AC⊥BC1
(2)VADC-A1B1C1=VABC-A1B1C1-VB1-BCD=
×3×4×4-
×4×
×
×3×4=20
(3)由题意可得:以CA、CB、CC1分别为x、y、z轴建立如图所示空间直角坐标系,
∵AC=3,BC=4,AA1=4,
∴C(0,0,0),D(
,2,0),B1(0,4,4),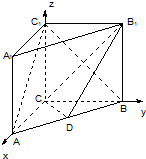
∴
=(
,2,0),
=(0,4,4)
平面CBB1C1的法向量
=(1,0,0),
设平面DB1C的法向量
=(x0,y0,-1),
则
,
的夹角的补角的大小就是二面角D-CB1-B的大小
则由
解得
=(-
,1,-1)
所以cos<
,
>=
=-
,
则tan<
,
>=-
∴二面角D-B1C-B的正切值为
∵AC2+BC2=AB2
∴AC⊥BC,
又AC⊥C1C,C1C∩BC=C
∴AC⊥平面BCC1;
∴AC⊥BC1
(2)VADC-A1B1C1=VABC-A1B1C1-VB1-BCD=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
(3)由题意可得:以CA、CB、CC1分别为x、y、z轴建立如图所示空间直角坐标系,
∵AC=3,BC=4,AA1=4,
∴C(0,0,0),D(
| 3 |
| 2 |

∴
| CD |
| 3 |
| 2 |
| CB1 |
平面CBB1C1的法向量
| n1 |
设平面DB1C的法向量
| n2 |
则
| n1 |
| n2 |
则由
|
| n2 |
| 4 |
| 3 |
所以cos<
| n1 |
| n2 |
| ||||
|
|
| 4 | ||
|
则tan<
| n1 |
| n2 |
3
| ||
| 4 |
∴二面角D-B1C-B的正切值为
3
| ||
| 4 |

练习册系列答案
相关题目