Question

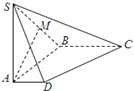
已知菱形ABCD的边长为2，对角线AC与BD交于点O，且∠ABC=120°，M为BC的中点．将此菱形沿对角线BD折成二面角A-BD-C．
（ I）求证：面AOC⊥面BCD；
（ II）若二面角A-BD-C为60°时，求直线AM与面AOC所成角的余弦值．

Answer 1

（ I）证明：因为四边形ABCD为菱形，
所以OA⊥BD，OC⊥BD，
所以

AO⊥BD CO⊥BD AO∩CO=O

⇒

BD⊥面AOC BD⊆面BCD

⇒面AOC⊥面BCD…（6分）
（ II）菱形沿对角线BD折成二面角A-BD-C后，仍然有AO⊥BD，CO⊥BD，
∴∠AOC是二面角A-BD-C的平面角，即∠AOC=60°…（8分）
作MK⊥OC，连接AK，如图所示：

因为MK∥BD，BD⊥面AOC，
所以MK⊥面AOC，
所以∠MAK是直线AM与面AOC所成的角…（10分）
因为菱形ABCD的边长为2，对角线AC与BD交于点O，且∠ABC=120°，
所以OC=AO=

3

，BD=

3

．
又因为MK⊥OC，M为BC的中点，
所以K为OC的中点，
所以OK=

3

2

，
所以在△AOK中，因为∠AOC=60°，
所以AK2=AO2+OK2-2AO•OK•cos∠AOK=

9

4

，所以AK=

3

2

．
在Rt△AMK中，
∵AK=

3

2

，MK=

1

2

BO=

1

2

，
∴AM=

10

2

，
∴cos∠MAK=

AK

MA

=

3

10

=

3 10

10

，
∴直线AM与面AOC所成角的余弦值是

3 10

10

…（14分）