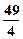题目内容
((本题满分15分)
已知三个函数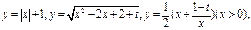 其中第二个函数和第三个函数中的
其中第二个函数和第三个函数中的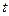 为同一个常数,且
为同一个常数,且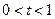 ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程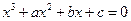 的三个根.
的三个根.
(Ⅰ) 求证: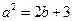 ;
;
(Ⅱ) 设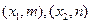 是函数
是函数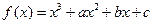 的两个极值点,求
的两个极值点,求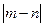 的取值范围.
的取值范围.
已知三个函数
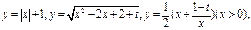 其中第二个函数和第三个函数中的
其中第二个函数和第三个函数中的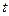 为同一个常数,且
为同一个常数,且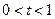 ,它们各自的最小值恰好是方程
,它们各自的最小值恰好是方程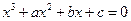 的三个根.
的三个根.(Ⅰ) 求证:
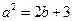 ;
;(Ⅱ) 设
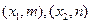 是函数
是函数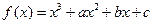 的两个极值点,求
的两个极值点,求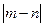 的取值范围.
的取值范围.解: (Ⅰ)三个函数的最小值依次为 ,由
,由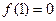 ,得
,得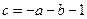 ,(2分)
,(2分)
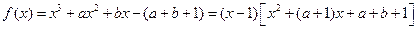 ,…(4分)
,…(4分)
故方程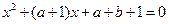 的两根是
的两根是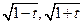 .
.
则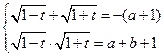 即
即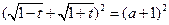 ,………(6分)
,………(6分)
故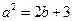 . …………………(7分)
. …………………(7分)
(Ⅱ) 依题意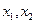 是方程
是方程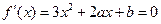 的两个根, …………(8分)
的两个根, …………(8分)
故有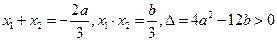 得
得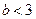 . ……(9分)
. ……(9分)
由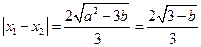 , ……………………… (10分)
, ……………………… (10分)
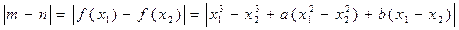
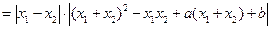
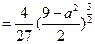 . ……………………………(13分)
. ……………………………(13分)
由(1)知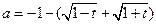 ,
,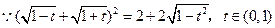
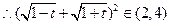 ,
,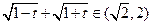
 ,
,
即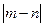 的取值范围
的取值范围 . ………………(15分)
. ………………(15分)
 ,由
,由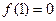 ,得
,得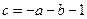 ,(2分)
,(2分)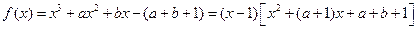 ,…(4分)
,…(4分)故方程
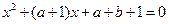 的两根是
的两根是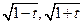 .
.则
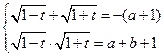 即
即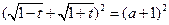 ,………(6分)
,………(6分)故
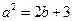 . …………………(7分)
. …………………(7分)(Ⅱ) 依题意
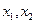 是方程
是方程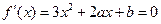 的两个根, …………(8分)
的两个根, …………(8分)故有
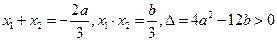 得
得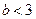 . ……(9分)
. ……(9分)由
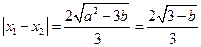 , ……………………… (10分)
, ……………………… (10分)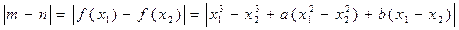
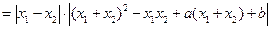
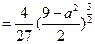 . ……………………………(13分)
. ……………………………(13分)由(1)知
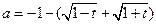 ,
,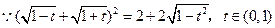
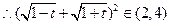 ,
,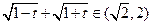
 ,
,即
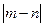 的取值范围
的取值范围 . ………………(15分)
. ………………(15分)略

练习册系列答案
相关题目
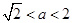 ,则函数
,则函数 的零点个数为 ( ▲ ) .
的零点个数为 ( ▲ ) . ,若
,若 ,则实数a的取值范围是
,则实数a的取值范围是 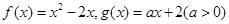 ,对
,对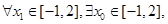 使
使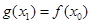 ,则
,则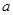 的取值范围是 ( ▲ )
的取值范围是 ( ▲ )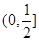
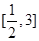
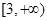

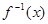 是函数
是函数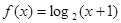 的反函数,若
的反函数,若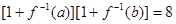 ,则f(a+b)的值为
,则f(a+b)的值为 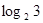
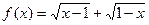 是 ( )
是 ( )
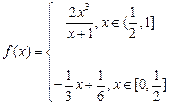 ,函数
,函数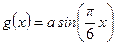
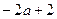 (a>0),若存在
(a>0),若存在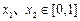 ,使得
,使得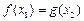 成立,则实数
成立,则实数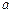 的取值范围是( )
的取值范围是( )
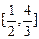
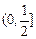
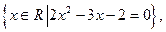 用列举法表示为____________.
用列举法表示为____________.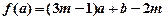 ,当
,当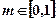 时,
时,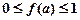 恒成立, 则
恒成立, 则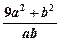 的最大值与最小值之和为
的最大值与最小值之和为