题目内容
设M为部分正整数组成的集合,数列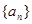 的首项
的首项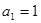 ,前n项和为
,前n项和为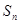 ,已知对任意整数k属于M,当n>k时,
,已知对任意整数k属于M,当n>k时,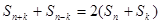 都成立。
都成立。
(1)设M={1},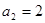 ,求
,求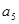 的值;
的值;
(2)设M={3,4},求数列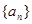 的通项公式。
的通项公式。
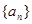 的首项
的首项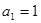 ,前n项和为
,前n项和为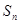 ,已知对任意整数k属于M,当n>k时,
,已知对任意整数k属于M,当n>k时,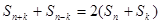 都成立。
都成立。(1)设M={1},
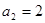 ,求
,求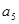 的值;
的值;(2)设M={3,4},求数列
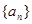 的通项公式。
的通项公式。(1)8 (2)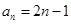
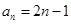
考察等差数列概念、和与通项关系、集合概念、转化与化归、分析问题与解决问题的能力,其中(1)是容易题,(2)是难题。
(1)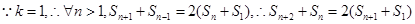 即:
即: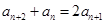
所以,n>1时,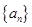 成等差,而
成等差,而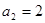 ,
,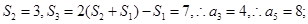
(2)由题意: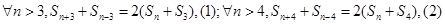 ,
,

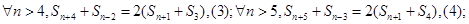
当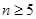 时,由(1)(2)得:
时,由(1)(2)得:
由(3)(4)得: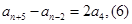
由(1)(3)得: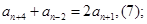
由(2)(4)得: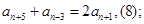
由(7)(8)知: 成等差,
成等差,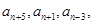 成等差;设公差分别为:
成等差;设公差分别为: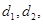
由(5)(6)得: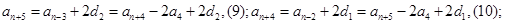
由(9)(10)得: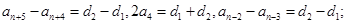
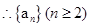 成等差,设公差为d,
成等差,设公差为d,
在(1)(2)中分别取n=4,n=5得: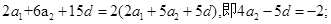
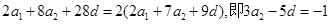
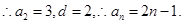
(1)
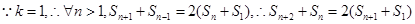 即:
即: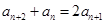
所以,n>1时,
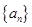 成等差,而
成等差,而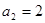 ,
,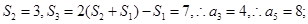
(2)由题意:
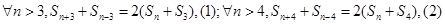 ,
,
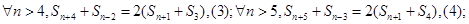
当
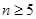 时,由(1)(2)得:
时,由(1)(2)得:
由(3)(4)得:
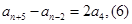
由(1)(3)得:
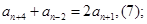
由(2)(4)得:
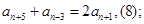
由(7)(8)知:
 成等差,
成等差,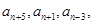 成等差;设公差分别为:
成等差;设公差分别为: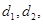
由(5)(6)得:
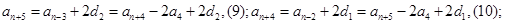
由(9)(10)得:
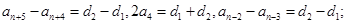
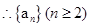 成等差,设公差为d,
成等差,设公差为d,在(1)(2)中分别取n=4,n=5得:
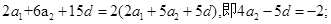
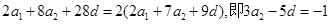
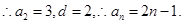

练习册系列答案
相关题目
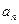 }为等差数列,公差d = -2,
}为等差数列,公差d = -2,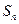 为其前n项和.若
为其前n项和.若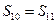 ,则
,则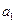 =( )
=( ) 定义如下:
定义如下: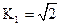 ,
, ,
, .
. 的值;
的值;  定义为:
定义为: ,
, ; ②证明:
; ②证明: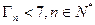 .
.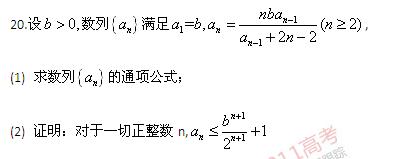
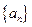 中,
中,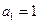 ,
,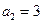 ,其前
,其前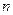 项和为
项和为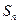 ,且当
,且当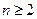 时,
时,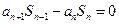 .
.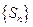 是等比数列;
是等比数列;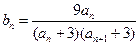 ,记数列
,记数列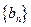 的前
的前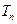 ,证明对于任意的正整数
,证明对于任意的正整数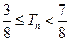 成立.
成立.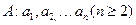 满足
满足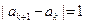
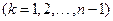 ,则称
,则称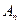 为
为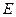 数列。记
数列。记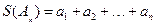 。
。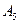 满足
满足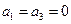 ;
;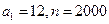 ,证明:
,证明: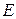 数列
数列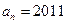 ;
;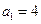 的
的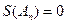 成立的
成立的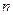 的最小值。
的最小值。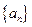 中,
中,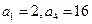 。
。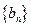 中,
中,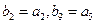 ,求数列
,求数列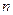 项和
项和 。
。