题目内容
本小题共13分)
若数列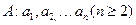 满足
满足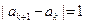
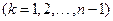 ,则称
,则称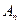 为
为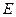 数列。记
数列。记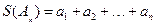 。
。
(Ⅰ)写出一个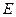 数列
数列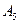 满足
满足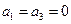 ;
;
(Ⅱ)若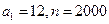 ,证明:
,证明: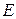 数列
数列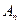 是递增数列的充要条件是
是递增数列的充要条件是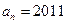 ;
;
(Ⅲ)在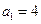 的
的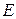 数列
数列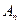 中,求使得
中,求使得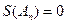 成立的
成立的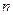 的最小值。
的最小值。
若数列
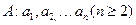 满足
满足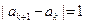
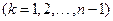 ,则称
,则称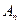 为
为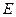 数列。记
数列。记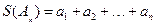 。
。(Ⅰ)写出一个
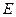 数列
数列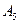 满足
满足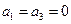 ;
;(Ⅱ)若
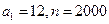 ,证明:
,证明: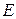 数列
数列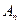 是递增数列的充要条件是
是递增数列的充要条件是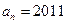 ;
;(Ⅲ)在
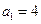 的
的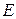 数列
数列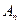 中,求使得
中,求使得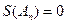 成立的
成立的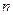 的最小值。
的最小值。略


练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
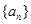 为等差数列,
为等差数列,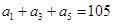 ,
,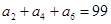 ,则
,则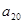 等于( )
等于( )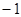
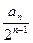 }的前n项和。
}的前n项和。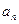 }的前n项和满足
}的前n项和满足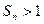 ,且
,且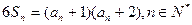
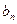 }满足
}满足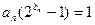 ,并记
,并记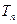 为{
为{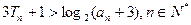
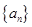 的前
的前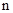 项和为
项和为 ,若
,若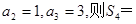 ( )
( )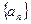 为等差数列,
为等差数列,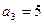 ,
,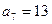 ,数列
,数列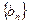 的前
的前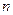 项和为
项和为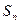 ,且有
,且有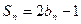
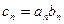 ,
,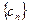 的前
的前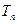 ,求
,求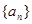 的首项
的首项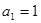 ,前n项和为
,前n项和为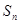 ,已知对任意整数k属于M,当n>k时,
,已知对任意整数k属于M,当n>k时,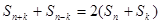 都成立。
都成立。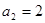 ,求
,求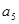 的值;
的值;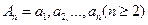 满足
满足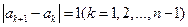 ,数列
,数列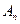 为
为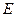 数列,记
数列,记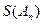 =
=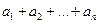 .
.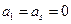 ,且
,且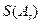 〉0的
〉0的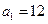 ,n=2000,证明:E数列
,n=2000,证明:E数列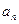 =2011;
=2011;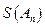 =0?如果存在,写出一个满足条件的E数列
=0?如果存在,写出一个满足条件的E数列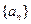 的前
的前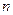 项和为
项和为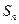 且
且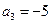 ,
,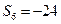 .
.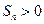 时最小的正整数
时最小的正整数