Question

【题目】已知变量，满足下列条件：．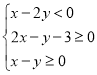

（1）求的最大值；

（2）求的最小值；

（3）求的最小值．

Answer 1

【答案】（1）无最大值．（2）无最小值．（3）最小值是3．

【解析】

根据题意作出可行域

（1）将改写成，即为直线在轴上的截距，根据可行域可得出结论.
（2）直线，变形为．问题转而求直线在轴上截距的最小值．根据可行域可得出结论.
（3）写成．即先求直线在轴上截距的最大值，从而求出的最小值,几何可行域可得出答案.

解 如图所示，画出直线（虚线）；（实线）；（实线）．

则不等式组满足的平面区域如图所示的阴影部分．

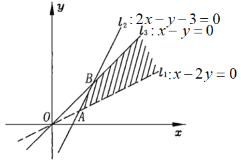
（1）将改写成，即为直线在轴上的截距，

求的最大值即求直线在轴上截距的最大值．

由于满足条件的平面区域不是封闭的．和的取值均无上界，故直线在轴上截距无最大值，即无最大值．

（2）直线，同理变形为．问题转而求直线在轴上截距的最小值．

当直线过时看似取最小值，但点不包括在平面区域内，故也无最小值．

（3）写成．即先求直线在轴上截距的最大值，从而求出的最小值．

由可得点坐标为，

作直线．平移可知过点时，直线在轴上截距最大，即此时最小．

将代入，得，

所以的最小值是3．