题目内容
(本小题满分10分)通过点A(0,a)的直线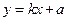 与圆
与圆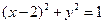 相交于不同的两点B、C,在线段BC上取一点P,使
相交于不同的两点B、C,在线段BC上取一点P,使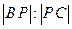 =
=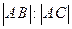 ,设点B在点C的左边,(1)试用a和k表示P点的坐标;(2)求k变化时P点的轨迹;(3)证明不论a取何值时,上述轨迹恒过圆内的一定点.
,设点B在点C的左边,(1)试用a和k表示P点的坐标;(2)求k变化时P点的轨迹;(3)证明不论a取何值时,上述轨迹恒过圆内的一定点.
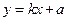 与圆
与圆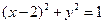 相交于不同的两点B、C,在线段BC上取一点P,使
相交于不同的两点B、C,在线段BC上取一点P,使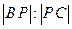 =
=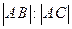 ,设点B在点C的左边,(1)试用a和k表示P点的坐标;(2)求k变化时P点的轨迹;(3)证明不论a取何值时,上述轨迹恒过圆内的一定点.
,设点B在点C的左边,(1)试用a和k表示P点的坐标;(2)求k变化时P点的轨迹;(3)证明不论a取何值时,上述轨迹恒过圆内的一定点.解:(1)
得

(2)由
 ,
, 的表达式中消去
的表达式中消去 得
得 ,∴点P的轨迹是直线
,∴点P的轨迹是直线 在圆内的部分。
在圆内的部分。(3)∴P点的轨迹恒过圆内的一定点
解:(1)设 ,依题意知,
,依题意知, ,
,
∴ , ∴
, ∴ …………………………………… 4分
…………………………………… 4分
由 ,整理得,
,整理得,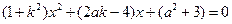
由
得 …………………………… 6分
…………………………… 6分
(2)由 ,
, 的表达式中消去
的表达式中消去 得
得 ,∴点P的轨迹是直线
,∴点P的轨迹是直线 在圆内的部分。……………………………………………………… 8分
在圆内的部分。……………………………………………………… 8分
(3)直线 恒过定点M(
恒过定点M( ,0),点M到圆心C(2,0)的距离
,0),点M到圆心C(2,0)的距离
 <r=1,∴该点在圆内 ∴P点的轨迹恒过圆内的一定点 ……… 10分
<r=1,∴该点在圆内 ∴P点的轨迹恒过圆内的一定点 ……… 10分
 ,依题意知,
,依题意知, ,
,∴
 , ∴
, ∴ …………………………………… 4分
…………………………………… 4分由
 ,整理得,
,整理得,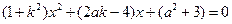
由

得
 …………………………… 6分
…………………………… 6分(2)由
 ,
, 的表达式中消去
的表达式中消去 得
得 ,∴点P的轨迹是直线
,∴点P的轨迹是直线 在圆内的部分。……………………………………………………… 8分
在圆内的部分。……………………………………………………… 8分(3)直线
 恒过定点M(
恒过定点M( ,0),点M到圆心C(2,0)的距离
,0),点M到圆心C(2,0)的距离 <r=1,∴该点在圆内 ∴P点的轨迹恒过圆内的一定点 ……… 10分
<r=1,∴该点在圆内 ∴P点的轨迹恒过圆内的一定点 ……… 10分
练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
 的边
的边 边所在直线的方程为
边所在直线的方程为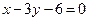
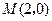 满足
满足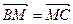 , 点
, 点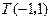 在AC边所在直线上
在AC边所在直线上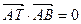 .
.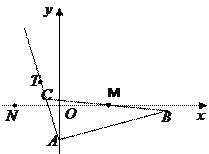
 过点
过点 ,且与
,且与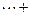 f(n)=
f(n)=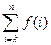 ,其中k, n为正整数且k
,其中k, n为正整数且k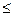 n
n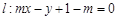 与圆C:
与圆C: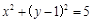 的位置关系是( )
的位置关系是( )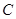 :
: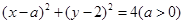 及直线
及直线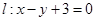 ,当直线
,当直线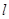 被
被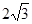 时,则
时,则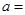
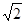 B
B 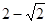 C
C 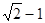 D
D 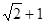
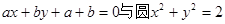 的位置关系 ( )
的位置关系 ( ) :
: 与圆
与圆 :
: 的位置关系是
的位置关系是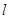 :
: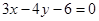 与圆
与圆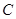 :
: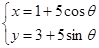 (θ为参数)相交所成的弦长为( )
(θ为参数)相交所成的弦长为( )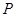 过定点
过定点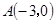 ,并且在定圆
,并且在定圆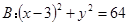 的内部与其相内切,求动圆圆心
的内部与其相内切,求动圆圆心



 与圆
与圆 的公共弦长为
的公共弦长为 ,a=_______
,a=_______