题目内容
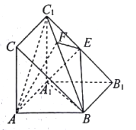
【题目】如图,直三棱柱ABC—A1B1C1中,侧面AA1B1B是正方形,AC丄侧面AA1B1B,AC=AB,点E是B1C1的中点.
(Ⅰ)求证:C1A∥平面EBA1;
(Ⅱ)若EF丄BC1,垂足为F,求二面角B—AF—A1的余弦值.
【答案】(1)见解析(2) ![]()
【解析】试题分析:(Ⅰ)由题意先证得EO//AC1,即可由线面平行的判定定理得出C1A∥平面EBA1;
(Ⅱ) 由已知AC丄底面AA1B1B,得A1C1丄底面AA1B1B,得C1A⊥AA1,C1A1⊥A1B1,又AA1⊥A1B1,故AA1,A1B1,A1C1两两垂直,建立空间直角坐标系,求得平面A1AF的法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() 设二面角B—AF—A1的平面角为θ,则
设二面角B—AF—A1的平面角为θ,则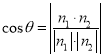 即得解.
即得解.
试题解析:
(Ⅰ)如图,连结![]() ,
, ![]() 交于
交于![]() ,连结
,连结![]() ,由
,由![]() 是正方形,易得O为AB1的中点,从而OE为
是正方形,易得O为AB1的中点,从而OE为![]() 的中位线,所以EO//AC1, 因为EO
的中位线,所以EO//AC1, 因为EO![]() 面EBA,C1A
面EBA,C1A![]() 面EBA1,所以C1A//平面EBA1
面EBA1,所以C1A//平面EBA1
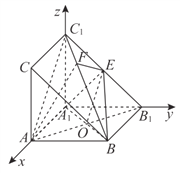
(Ⅱ)由已知AC丄底面AA1B1B,得A1C1丄底面AA1B1B,
得C1A⊥AA1,C1A1⊥A1B1,又AA1⊥A1B1,故AA1,A1B1,A1C1两两垂直,
如图,分别以AA1,A1B1,A1C1所在直线为x,y,z轴,A1为原点建立空间直角坐标系,
设AA1=2,则A1 (0,0,0) ,A(2,0,0),C1(0,0,2),E(0,1,1),B(2,2,0),
则![]() ,
, ![]() ,
, ![]() ,
,
设![]() ,则由
,则由![]() ,
,
得![]() ,即得
,即得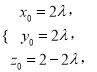
于是![]() ,所以
,所以![]()
又![]() ,所以
,所以![]() ,解得
,解得![]() ,
,
所以![]() ,
,
设平面A1AF的法向量是![]() ,则
,则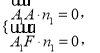 即
即![]()
令![]() ,则
,则![]() ,
,
又平面![]() 的一个法向量为
的一个法向量为![]() ,则
,则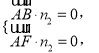 即
即![]()
令![]() ,得
,得![]()
设二面角B—AF—A1的平面角为θ,则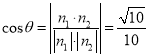
由![]() ,面
,面![]() 面
面![]() ,可知
,可知![]() 为锐角,
为锐角,
即二面角B—AF—A1的余弦值为![]() .
.

【题目】语音交互是人工智能的方向之一,现在市场上流行多种可实现语音交互的智能音箱,它们可以通过语音交互满足人们的部分需求.经市场调查,某种新型智能音箱的广告费支出x(万元)与销售额y(单位:万元)之间有如下对应数据:
x | 1 | 4 | 5 | 6 | 9 |
y | 20 | 35 | 50 | 65 | 80 |
(1)求y关于x的线性回归方程(数据精确到0.01);
(2)利用(1)中的回归方程,预测广告费支出10万元时的销售额.
附:回归直线的斜率和截距的最小二乘估计公式分别为: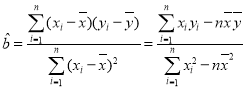 ,
,![]() .
.
【题目】通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:
男 | 女 | 总计 | |
爱好 | 40 | 20 | 60 |
不爱好 | 20 | 30 | 50 |
总计 | 60 | 50 | 110 |
由![]() 算得,
算得,![]()
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
参照附表,得到的正确结论是 ( )
A. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别有关”
B. 在犯错误的概率不超过1%的前提下,认为“爱好该项运动与性别无关”
C. 有99.9%以上的把握认为“爱好该项运动与性别有关”
D. 有99.9%以上的把握认为“爱好该项运动与性别无关”
【题目】某个调查小组在对人们的休闲方式的一次调查中,共调查了150人,其中男性45人,女性55人。女性中有35人主要的休闲方式是室内活动,另外20人主要的休闲方式是室外运动;男性中15人主要的休闲方式是室内活动,另外30人主要的休闲方式是室外运动。
参考数据:![]()
| 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(1)根据以上数据建立一个![]() 的列联表;
的列联表;
(2)能否在犯错误的概率不超过0.005的前提下认为休闲方式与性别有关?