题目内容
20.函数f(x)=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|的零点个数为( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 函数f(x)=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|的零点个数为y=|ln(x+1)|与y=sin2x的图象的交点的个数,作图并利用三角函数的图象特征求解.
解答 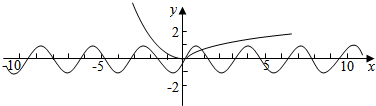 解:f(x)=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|=sin2x-|ln(x+1)|
解:f(x)=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|=sin2x-|ln(x+1)|
函数f(x)=4cos2$\frac{x}{2}$cos($\frac{π}{2}$-x)-2sinx-|ln(x+1)|的零点个数为y=|ln(x+1)|与y=sin2x的图象的交点的个数,
作函数y=|ln(x+1)|与y=sin2x的图象,可得零点个数为2.
故选:B.
点评 本题考查了函数的图象的应用及函数的零点的个数的判断,属于基础题.

练习册系列答案
相关题目
9.设x∈R,则“|x-2|<1”是“x2+x>0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
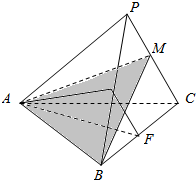 在三棱锥P-ABC中,AP=AC,BP=BC,E、F、M分别是PB、BC、CP的中点,求证:平面AEF⊥平面ABM.
在三棱锥P-ABC中,AP=AC,BP=BC,E、F、M分别是PB、BC、CP的中点,求证:平面AEF⊥平面ABM.