Question

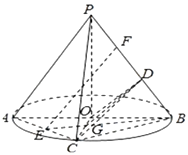
【题目】在如图所示的圆锥中，OP是圆锥的高，AB是底面圆的直径，点C是弧AB的中点，E是线段AC的中点，D是线段PB的中点，且PO=2，OB=1．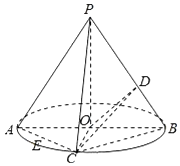

（1）试在PB上确定一点F，使得EF∥面COD，并说明理由；
（2）求点A到面COD的距离．

Answer 1

【答案】
（1）解：连接BE，设BE∩OC=G，由题意G为△ABC的重心，∴ =2，

连接DG，

∵EF∥平面COD，EF平面BEF，平面BEF∩平面COD=DG，

∴EF∥DG，

∴ = =2，

又BD=DP，∴DF=PF= PB．

∴点F是PB上靠近点P的四等分点．

（2）解：由PO⊥平面ABC，OC平面ABC，

∴OC⊥PO，又点C是弧AB的中点，OC⊥AB，∴OC⊥平面POB．

OD平面POB，∴OC⊥OD．

S△COD= OCOD= = ．

∵VA﹣OCD=VD﹣AOC，∴ S△CODd= PO，

∴ d= ，

∴点A到面COD的距离 ．

【解析】（1）连接BE，设BE∩OC=G，由题意G为△ABC的重心，可得 =2，连接DG，利用EF∥平面COD，可得EF∥DG，进而得出F点的位置．（2）由PO⊥平面ABC，可得OC⊥PO，利用线面面面垂直的判定与性质定理可得OC⊥平面POB．OC⊥OD．利用VA﹣OCD=VD﹣AOC ， 即可得出．