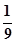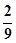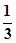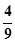题目内容
设a∈{1,2,3,4},b∈{2,4,8,12},则函数f(x)=x3+ax-b在区间[1,2]上有零点的概率为( )
A.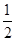 | B.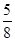 | C.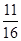 | D.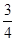 |
C
∵f(x)=x3+ax-b,∴f′(x)=3x2+a.∵a∈{1,2,3,4},∴f′(x)>0,∴函数f(x)在区间[1,2]上为增函数.若存在零点,则解得a+1≤b≤8+2a.因此可使函数在区间[1,2]上有零点的有:a=1,2≤b≤10,故b=2,b=4,b=8,a=2,3≤b≤12,故b=4,b=8,b=12,a=3,4≤b≤14,故b=4,b=8,b=12.a=4,5≤b≤16,故b=8,b=12.根据古典概型可得有零点的概率为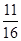 .
.
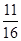 .
.
练习册系列答案
相关题目
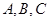 和3名女同学
和3名女同学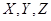 ,其年级情况如下表:
,其年级情况如下表: 为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件
为事件“选出的2人来自不同年级且恰有1名男同学和1名女同学”,求事件