题目内容
【题目】设函数f(x)是定义在R上的偶函数,对任意x∈R,都有f(x)=f(x+4),且当x∈[﹣2,0]时,f(x)=( ![]() )x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
)x﹣1,若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,则a的取值范围是( )
A.( ![]() ,2)
,2)
B.( ![]() ,2)
,2)
C.[ ![]() ,2)
,2)
D.( ![]() ,2]
,2]
【答案】B
【解析】解:设x∈[0,2],则﹣x∈[﹣2,0],
∴f(﹣x)=( ![]() )﹣x﹣1=2x﹣1,
)﹣x﹣1=2x﹣1,
∵f(x)是定义在R上的偶函数,
∴f(x)=f(﹣x)=2x﹣1.
∵对任意x∈R,都有f(x)=f(x+4),
∴当x∈[2,4]时,(x﹣4)∈[﹣2,0],∴f(x)=f(x﹣4)=xx﹣4﹣1;
当x∈[4,6]时,(x﹣4)∈[0,2],∴f(x)=f(x﹣4)=2x﹣4﹣1.
∵若在区间(﹣2,6]内关于x的方程f(x)﹣loga(x+2)=0(a>1)恰有三个不同的实数根,
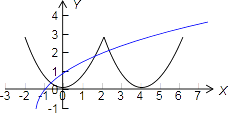
∴函数y=f(x)与函数y=loga(x+2)在区间(﹣2,6]上恰有三个交点,
通过画图可知:恰有三个交点的条件是 ![]() ,解得:
,解得: ![]() <a<2,
<a<2,
即 ![]() <a<2,因此所求的a的取值范围为(
<a<2,因此所求的a的取值范围为( ![]() ,2).
,2).
所以答案是:B
【考点精析】掌握函数奇偶性的性质是解答本题的根本,需要知道在公共定义域内,偶函数的加减乘除仍为偶函数;奇函数的加减仍为奇函数;奇数个奇函数的乘除认为奇函数;偶数个奇函数的乘除为偶函数;一奇一偶的乘积是奇函数;复合函数的奇偶性:一个为偶就为偶,两个为奇才为奇.

【题目】某市家庭煤气的使用量x(m3)和煤气费f(x)(元) 满足关系f(x)= ![]() ,已知某家庭今年前三个月的煤气费如表:
,已知某家庭今年前三个月的煤气费如表:
月份 | 用气量 | 煤气费 |
一月份 | 4m3 | 4 元 |
二月份 | 25m3 | 14 元 |
三月份 | 35m3 | 19 元 |
若四月份该家庭使用了20m3的煤气,则其煤气费为( )元.
A.10.5
B.10
C.11.5
D.11