题目内容
设F1,F2是椭圆E: +
+ =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x= 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
 +
+ =1(a>b>0)的左、右焦点,P为直线x=
=1(a>b>0)的左、右焦点,P为直线x= 上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )
上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为( )A. | B. | C.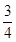 | D. |
C
如图所示,设直线x= a与x轴的交点为Q,
a与x轴的交点为Q,
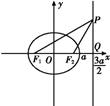
由题意可知,
∠F2F1P=∠F1PF2=30°,
|PF2|=|F1F2|=2c,
∴∠PF2Q=60°,∠F2PQ=30°.
∴|F2Q|=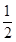 |PF2|.
|PF2|.
即 a-c=
a-c=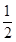 ·2c,
·2c,
∴e=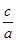 =
=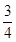 .
.
 a与x轴的交点为Q,
a与x轴的交点为Q,
由题意可知,
∠F2F1P=∠F1PF2=30°,
|PF2|=|F1F2|=2c,
∴∠PF2Q=60°,∠F2PQ=30°.
∴|F2Q|=
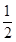 |PF2|.
|PF2|.即
 a-c=
a-c=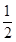 ·2c,
·2c,∴e=
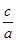 =
=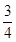 .
.
练习册系列答案
相关题目
 +
+ =1(a>b>0)的焦距为4,且过点P(
=1(a>b>0)的焦距为4,且过点P( ,
, ).
). |=|
|=| |?若存在,求出D点的坐标;若不存在,说明理由.
|?若存在,求出D点的坐标;若不存在,说明理由.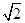 ,0),(
,0),( .直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P.
.直线y=t与椭圆C交于不同的两点M,N,以线段MN为直径作圆P,圆心为P. +
+ =1上有两个动点P、Q,E(3,0),EP⊥EQ,则
=1上有两个动点P、Q,E(3,0),EP⊥EQ,则 ·
· 的最小值为( )
的最小值为( )
 +
+ =1(a>b>0)的两个焦点,P为椭圆C上一点,且
=1(a>b>0)的两个焦点,P为椭圆C上一点,且 ⊥
⊥ ,若△PF1F2的面积为9,则b= .
,若△PF1F2的面积为9,则b= . 的焦点分别为
的焦点分别为 和
和 ,点
,点 在椭圆上,如果线段
在椭圆上,如果线段 的中点在
的中点在 轴上,那么
轴上,那么 。
。 ·
· =
= ,则点P的轨迹是( )
,则点P的轨迹是( )