Question

已知数列{a_n}的通项公式a_n=an=

2n-1，(k≤n≤) an-4，(n＞4)

，计算其前102项和的算法流程图如图所示，图中①，②应该填

 

、

 

．

Answer 1

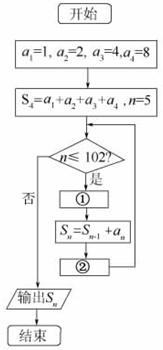
分析：由已知中该程序的功能是计算数列a_n前102项和的算法，根据循环体中应有使循环结束的语句，得出②中应填由循环变量构成的：“n=n+1”，根据数列的周期性，可知①应填给a_n赋值的语句a_n=a_n-4，由此易给出条件中填写的语句．

解答：解析：算法流程图中用的循环体中应有使循环结束的语句，
故应有n=1使原来的n的值增加1，故应在求和后，
所以应填在②中，而①应填给a_n赋值的语句a_n=a_n-4．
故答案为：a_n=a_n-4；n=n+1．

点评：算法是新课程中的新增加的内容，也必然是新高考中的一个热点，应高度重视．程序填空也是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．其中前两点考试的概率更大．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误．