题目内容
用长为18 m的钢条围成一个长方体容器的框架,如果所制的容器的长与宽之比为2∶1,那么高为多少时容器的容积最大?并求出它的最大容积.
容器高为1.5 m时容器的容积最大,最大容积为3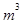 .
.
解析试题分析:设长方体的宽为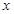 m, 长为2x m,高为
m, 长为2x m,高为 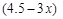 m,由实际意义得出
m,由实际意义得出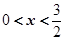 ,长方体体积可写出容积
,长方体体积可写出容积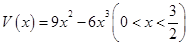 ,对
,对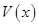 求导
求导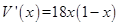 ,知0<x<1时,V′(x)>0;当
,知0<x<1时,V′(x)>0;当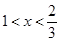 时,V′(x)<0,则
时,V′(x)<0,则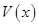 在
在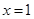 时有最大值,求之得最大容积.
时有最大值,求之得最大容积.
解:设长方体的宽为x m,则长为2x m,高为 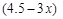 m,
m,
由 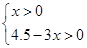 解得
解得  , 3分
, 3分
故长方体的容积为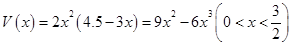 6分
6分
从而 V′(x)=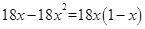 ,
,
令V′(x)=0,解得x=1或x=0 (舍去), 8分
当0<x<1时,V′(x)>0;
当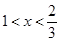 时,V′(x)<0,
时,V′(x)<0,
故在x=1处V(x)取得极大值,并且这个极大值就是V(x)的最大值,
从而最大体积为V(1)=9×12-6×13 = 3 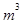 , 10分
, 10分
此时容器的高为4.5-3=1.5 m,
因此,容器高为1.5 m时容器的容积最大,最大容积为3 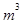 . 12分
. 12分
考点:利用导数求函数的最值,函数的应用.

练习册系列答案
相关题目
 (
(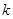 为常数,
为常数,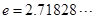 是自然对数的底数).
是自然对数的底数).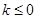 时,求函数
时,求函数 的单调区间;
的单调区间;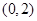 内存在两个极值点,求
内存在两个极值点,求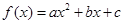 的图像过点
的图像过点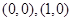 和
和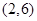 ,直线
,直线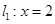 ,直线
,直线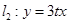 (其中
(其中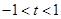 ,
,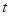 为常数);若直线
为常数);若直线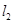 与函数
与函数 的图像以及直线
的图像以及直线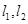 与函数
与函数 ;
;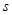 关于
关于 的解析式;
的解析式; 可作曲线
可作曲线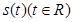 的三条切线,求实数
的三条切线,求实数 的取值范围.
的取值范围.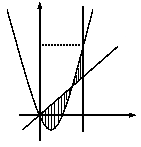
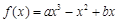 (
(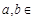 R),
R),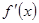 为其导函数,且
为其导函数,且 时
时 有极小值
有极小值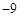 .
.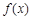 的单调递减区间;
的单调递减区间;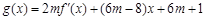 ,
,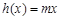 ,当
,当 时,对于任意x,
时,对于任意x,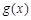 和
和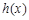 的值至少有一个是正数,求实数m的取值范围;
的值至少有一个是正数,求实数m的取值范围; (
( 为正整数)对任意正实数
为正整数)对任意正实数 恒成立,求
恒成立,求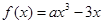 .
.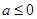 时,求函数
时,求函数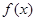 单调区间;
单调区间; ,求
,求 的值.
的值.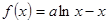 .
.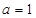 时,求
时,求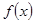 的极值;
的极值;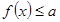 对
对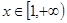 恒成立,求实数
恒成立,求实数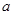 的取值范围.
的取值范围.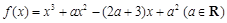 .
.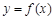 在
在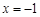 处的切线与直线
处的切线与直线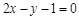 平行,求a的值;
平行,求a的值;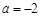 时,求
时,求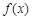 的单调区间.
的单调区间. .
.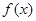 在
在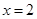 时取得极值,求实数
时取得极值,求实数 的值;
的值;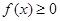 对任意
对任意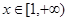 恒成立,求实数
恒成立,求实数 ≈1.6,e0.3≈1.3)。
≈1.6,e0.3≈1.3)。