题目内容
（本小题满分10分）
求原点到曲线C:(θ为参数)的最短距离.
求原点到曲线C:(θ为参数)的最短距离.
略
解法一:将参数方程化为普通方程得:
(x-3)2+(y+2)2="4, " ……………………………………4分
它是以C(3,-2)为圆心,以2为半径的圆.
∴|OC|== ……………………………………8分
由图形可知:原点到圆上的点的最短距离为:|OC|-2=-2 ………10分
解法二:设P(3+2sinθ,-2+2cosθ), …………………………………2分
令F(x)=|x+3|+|x-7|
不等式①的解集为R等价于10a<Fmin(x)
由绝对值的三角不等式知: |x+3|+|x-7|≥|x+3-x+7|=10…………8分
(x-3)2+(y+2)2="4, " ……………………………………4分
它是以C(3,-2)为圆心,以2为半径的圆.
∴|OC|== ……………………………………8分
由图形可知:原点到圆上的点的最短距离为:|OC|-2=-2 ………10分
解法二:设P(3+2sinθ,-2+2cosθ), …………………………………2分
令F(x)=|x+3|+|x-7|
不等式①的解集为R等价于10a<Fmin(x)
由绝对值的三角不等式知: |x+3|+|x-7|≥|x+3-x+7|=10…………8分
练习册系列答案
新思维寒假作业系列答案
相关题目
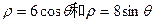，求这两个圆的圆心距。
与圆
（
为参数），试判断它们的公共点个数。
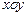中，直线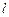
的参数方程为
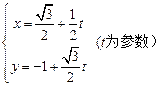，曲线C的参数方程为
.
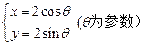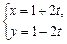（t为参数）被圆
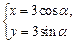（α为参数）截得的弦长．
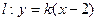与曲线
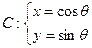（参数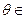
R）有唯一的公共点，则实数
． 
（
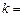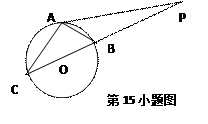
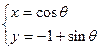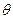为参数）的普通方程是__________，如果曲线C与直线
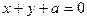有公共点，那么实数
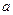的取值范围是_________．
（
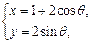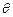为参数）化成普通
方程为 ．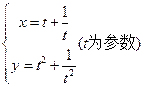
化为普通方程，所得方程是 _________.