题目内容
在△ABC中，若∠B=60°，AC=3，AB=
，则∠A= ．
【答案】分析：根据正弦定理求出sinC的值，然后根据特殊角的三角函数值求出∠C的度数，然后利用三角形的内角和定理求出∠A的度数即可．
解答：解：根据正弦定理得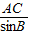
=
即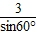
=
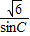解得sinC=
=
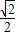，则∠C=45°或135°；
当∠C=45°时，由∠B=60°和三角形的内角和定理得到∠A=180°-45°-60°=75°；当∠C=135°时，因为∠B=60°，与三角形的内角和定理矛盾，舍去．所以∠A=75°．
故答案为：75°
点评：考查学生灵活正弦定理及三角形的内角和定理解决数学问题的能力．做题时应讨论∠C的取值．
解答：解：根据正弦定理得
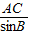=即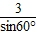=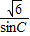解得sinC==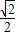，则∠C=45°或135°；当∠C=45°时，由∠B=60°和三角形的内角和定理得到∠A=180°-45°-60°=75°；当∠C=135°时，因为∠B=60°，与三角形的内角和定理矛盾，舍去．所以∠A=75°．
故答案为：75°
点评：考查学生灵活正弦定理及三角形的内角和定理解决数学问题的能力．做题时应讨论∠C的取值．
练习册系列答案
相关题目