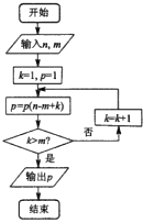
题目内容
【题目】如图△ABC是等腰三角形,BA=BC,DC⊥平面ABC,AE∥DC,若AC=2且BE⊥AD,则( ) 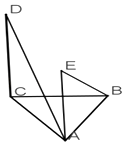
A.AB+BC有最大值
B.AB+BC有最小值
C.AE+DC有最大值
D.AE+DC有最小值
【答案】D
【解析】解:取AC的中点O,连接OB,OE,则OB⊥AC,
∵DC⊥平面ABC,∴DC⊥OB,
∵DC∩AC=C,
∴OB⊥平面ADC,
∴OB⊥AD,
∵BE⊥AD,OB∩BE=B,
∴AD⊥平面BOE,
∴AD⊥OE,
∴∠AEO=∠CAD,
∴ ![]() =
= ![]() ,
,
∴AE= ![]() ,
,
∴AE+CD=CD+ ![]() ≥2
≥2 ![]() ,当且仅当CD=
,当且仅当CD= ![]() 时,AE+DC有最小值,
时,AE+DC有最小值,
故选D.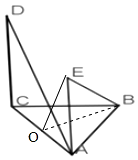
【考点精析】本题主要考查了直线与平面垂直的判定的相关知识点,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能正确解答此题.

练习册系列答案
 每课必练系列答案
每课必练系列答案 巧学巧练系列答案
巧学巧练系列答案
相关题目