题目内容
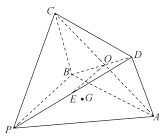
【题目】如图,矩形ABCD 中,AD⊥平面ABE,AE=FB=BC=2,F为CE上的点,且BF⊥平面ACE,AC,BD交于G点 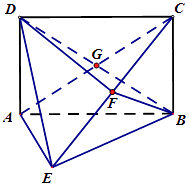
(1)求证:AE∥平面BFD
(2)求证:AE⊥平面BCE
(3)求三棱柱C﹣BGF的体积.
【答案】
(1)证明:依题意可知:G是AC中点,
∵BF⊥平面ACE,则CE⊥BF,而BC=BE,∴F是EC中点.
在△ABC中,FG∥AE,∴AE∥平面BFD
(2)证明:∵AD⊥平面ABE,AD∥BC,
∴BC⊥平面ABE,则AE⊥BC.
又∵BF⊥平面ACE,则CE⊥BF,
∴AE⊥平面BCE
(3)∵AE∥平面BFD,∴AE∥FG,而AE⊥平面BCG,
∴FG⊥平面BCE,∴GF⊥平面BCF.
∵G是AC的中点,∴F是CE的中点,且FG= ![]() ,
,
∵BF⊥平面ACE,∴BF⊥CE.
∴在Rt△BCE中,BF=CF= ![]() .
.
∴ ![]() ,
,
则 ![]() .
.
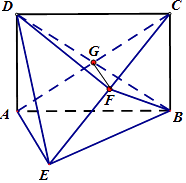
【解析】(1)依题意可知G是AC中点,由BF⊥平面ACE,得CE⊥BF,再由BC=BE,可得F是EC中点,得到FG∥AE,由线面平行的判定得AE∥平面BFD.(2)由AD⊥平面ABE,AD∥BC,可得BC⊥平面ABE,进一步得到AE⊥BC.结合BF⊥平面ACE,得CE⊥BF,由线面垂直的判定得AE⊥平面BCE;(3)由已知可得GF⊥平面BCF.解直角三角形求得△BCF的面积,然后利用等积法求得三棱柱C﹣BGF的体积.
【考点精析】根据题目的已知条件,利用直线与平面垂直的判定的相关知识可以得到问题的答案,需要掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.

练习册系列答案
相关题目