题目内容
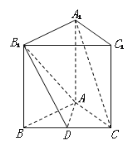
【题目】如图,在四棱锥P﹣ABCD中,已知PA⊥平面ABCD,AD∥BC,AD⊥AB,PA=AD=2BC=2AB=2. 
(1)求证:平面PAC⊥平面PCD;
(2)若E是PD的中点,求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比.
【答案】
(1)证明:∵PA⊥平面ABCD,CD平面ABCD,
∴PA⊥CD.
取AD中点H,连接CH,则CH⊥AD,CH=AB=HD.
∴∠ACH=∠DCH=45°,
∴AC⊥CD,
∵PA∩AC=A,
∴CD⊥平面PAC,
∵CD平面PAC,
∴平面PAC⊥平面PCD;
(2)证明:解:取PD中点E,PA中点F,连接EF,BE,则EF∥AD,
∵BC∥AD,
∴EF∥BC,
∴B,C,E,F四点共面.
故平面BCE将四棱锥P﹣ABCD分成的上部分为四棱锥P﹣BCEF,下部分为多面体EFABCD.
易知ABF﹣HCE为直三棱柱,CH⊥平面PAD.
∴V2=VABF﹣HCE+VC﹣DEH=S△ABFBC+ ![]() =
= ![]() +
+ ![]()
= ![]() =
= ![]() ,
,
∵VP﹣ABCD= ![]() =
= ![]() =1,
=1,
∴V1=1﹣ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() .
.

【解析】(1)取AD中点H,连接CH,则CH⊥AD,CH=AB=HD,证明CD⊥平面PAC,即可证明求证:平面PAC⊥平面PCD;(2)证明B,C,E,F四点共面,故平面BCE将四棱锥P﹣ABCD分成的上部分为四棱锥P﹣BCEF,下部分为多面体EFABCD.易知ABF﹣HCE为直三棱柱,CH⊥平面PAD,利用体积公式,即可求平面BCE将四棱锥P﹣ABCD分成的上下两部分体积V1、V2之比.
【考点精析】解答此题的关键在于理解平面与平面垂直的判定的相关知识,掌握一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目