题目内容
2.已知α,β是两个不同的平面,有下列三个条件:①存在一个平面γ,γ⊥α,γ∥β;
②存在一条直线a,a?α,a⊥β;
③存在两条垂直的直线a,b,a⊥β,b⊥α.
其中,所有能称为“α⊥β”的充要条件的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ①③ |
分析 由空间中线线、线面、面面间的位置关系得①②都是“α⊥β”的充分不必要条件,③是“α⊥β”的充要条件.
解答 解:由α,β是两个不同的平面,知: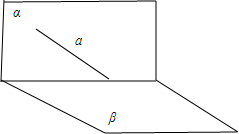
①存在一个平面γ,γ⊥α,γ∥β⇒α⊥β,反之则不成立,故①不正确;
②存在一条直线a,a?α,a⊥β⇒α⊥β,反之则不成立,
如图,α⊥β,a?α,但a不垂直于平面β,故②不正确;
③存在两条垂直的直线a,b,a⊥β,b⊥α?α⊥β,故③正确.
故选:C.
点评 本题考查两个平面垂直的充要条件的判断,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
10.已知函数f(x)=sin(ωx+$\frac{π}{6}$),其中ω>0,若f($\frac{π}{6}$)=f($\frac{π}{3}$),且f(x)在区间($\frac{π}{6}$,$\frac{π}{3}$)上有最小值、无最大值,则ω等于( )
| A. | $\frac{40}{3}$ | B. | $\frac{28}{3}$ | C. | $\frac{16}{3}$ | D. | $\frac{4}{3}$ |
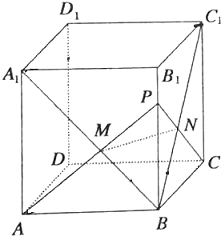 如图,在长方体ABCD-A1B1C1D1中,点P∈BB1(P不与B,B1重合).PA∩A1B=M,PC∩BC1=N.
如图,在长方体ABCD-A1B1C1D1中,点P∈BB1(P不与B,B1重合).PA∩A1B=M,PC∩BC1=N.