题目内容
7.已知梯形ABCD的各顶点依次在半径为1的圆上,下底AB是直径,$\overrightarrow{AC}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,其中λ,μ∈R,则λ+μ的取值范围是(1,2).分析 以AB所在直线为x轴,AB的垂直平分线为y轴,建立坐标系,设∠COB=α(α∈(0,$\frac{π}{2}$)),利用$\overrightarrow{AC}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,求出λ+μ=cosα+1,即可求出λ+μ的取值范围.
解答 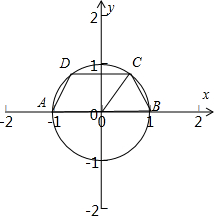 解:以AB所在直线为x轴,AB的垂直平分线为y轴,建立坐标系,设∠COB=α(α∈(0,$\frac{π}{2}$)),则
解:以AB所在直线为x轴,AB的垂直平分线为y轴,建立坐标系,设∠COB=α(α∈(0,$\frac{π}{2}$)),则
A(-1,0),B(1,0),C(cosα,sinα),D(-cosα,sinα),
∵$\overrightarrow{AC}$=λ$\overrightarrow{AB}$+μ$\overrightarrow{AD}$,
∴(cosα+1,sinα)=λ(2,0)+μ(-cosα+1,sinα),
∴2λ+μ(-cosα+1)=cosα+1,μ=1
∴λ=cosα,
∴λ+μ=cosα+1∈(1,2).
故答案为:(1,2).
点评 本题考查平面向量基本定理的运用,考查坐标法,考查学生分析解决问题的能力,正确建立坐标系是关键.

练习册系列答案
相关题目
17.执行如图所示的程序框图,则输出的A的值为( )


| A. | 7 | B. | 15 | C. | 29 | D. | 31 |
18.点集{(x,y)|(|x|-1)2+y2=4}表示的图形是一条封闭的曲线,这条封闭曲线所围成的区域面积是( )
| A. | $\frac{16π}{3}+2\sqrt{3}$ | B. | $\frac{16π}{3}+4\sqrt{3}$ | C. | $\frac{24π}{3}+2\sqrt{3}$ | D. | $\frac{24π}{3}+4\sqrt{3}$ |
2.已知α,β是两个不同的平面,有下列三个条件:
①存在一个平面γ,γ⊥α,γ∥β;
②存在一条直线a,a?α,a⊥β;
③存在两条垂直的直线a,b,a⊥β,b⊥α.
其中,所有能称为“α⊥β”的充要条件的序号是( )
①存在一个平面γ,γ⊥α,γ∥β;
②存在一条直线a,a?α,a⊥β;
③存在两条垂直的直线a,b,a⊥β,b⊥α.
其中,所有能称为“α⊥β”的充要条件的序号是( )
| A. | ① | B. | ② | C. | ③ | D. | ①③ |
19.某市场调查员在同一天对本市的5家商场的某商品的一天销售量及其价格进行调查,5家商场的售价x(元)和销售量y(件)之间的一组数据如下表所示:
由散点图可知,销售量y与价格x之间有较好的线性相关关系,且回归直线方程是$\widehat{y}$=-3.2x+4a,则实数a等于( )
| 价格x(元) | 9 | 9.5 | 10 | 10.5 | 11 |
| 销售量y(件) | 11 | a | 8 | 6 | 5 |
| A. | 7 | B. | 8.5 | C. | 9 | D. | 10 |
17.已知函数f(x)=|xex|,且方程f2(x)+2af(x)+1=0(a∈R)有四个实数根,则a的取值范围为( )
| A. | (-∞,-$\frac{{e}^{2}+1}{2e}$) | B. | (-$\frac{{e}^{2}+1}{e}$,-2) | C. | (-2,0) | D. | ($\frac{{e}^{2}+1}{2e},+∞$) |
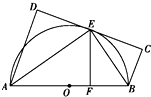 如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.
如图,AB为☉O的直径,直线CD与☉O相切于E,AD垂直CD于D,BC垂直CD于C,EF垂直AB于F,连接AE,BE.求证:∠FEB=∠CEB.