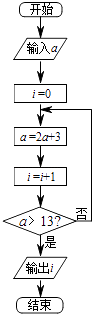题目内容
【题目】已知实数![]() ,函数
,函数![]() .
.
(1)当![]() 时,求
时,求![]() 的最小值;
的最小值;
(2)当![]() 时,判断
时,判断![]() 的单调性,并说明理由;
的单调性,并说明理由;
(3)求实数![]() 的范围,使得对于区间
的范围,使得对于区间 上的任意三个实数
上的任意三个实数![]() ,都存在以
,都存在以![]() 为边长的三角形.
为边长的三角形.
【答案】(1)2;(2)递增;(3).
【解析】
试题(1)研究函数问题,一般先研究函数的性质,如奇偶性,单调性,周期性等等,如本题中函数![]() 是偶函数,因此其最小值我们只要在
是偶函数,因此其最小值我们只要在![]() 时求得即可;(2)
时求得即可;(2)![]() 时,
时,![]() 可化简为
可化简为![]() ,下面我们只要按照单调性的定义就可证明在
,下面我们只要按照单调性的定义就可证明在![]() 上函数是单调递增的,当然在
上函数是单调递增的,当然在![]() 上是递减的;(3)处理此问题,首先通过换元法把问题简化,设
上是递减的;(3)处理此问题,首先通过换元法把问题简化,设![]() ,则函数
,则函数![]() 变为
变为![]() ,问题变为求实数
,问题变为求实数![]() 的范围,使得在区间
的范围,使得在区间![]() 上,恒有
上,恒有![]() .对于函数
.对于函数![]() ,我们知道,它在
,我们知道,它在![]() 上递减,在
上递减,在![]() 上递增,故我们要讨论它在区间
上递增,故我们要讨论它在区间![]() 上的最大(小)值,就必须分类讨论,分类标准显然是
上的最大(小)值,就必须分类讨论,分类标准显然是![]() ,
,![]() ,
,![]() ,在
,在![]() 时还要讨论最大值在区间
时还要讨论最大值在区间![]() 的哪个端点取得,也即共分成四类.
的哪个端点取得,也即共分成四类.
试题解析:易知![]() 的定义域为
的定义域为![]() ,且
,且![]() 为偶函数.
为偶函数.
(1)![]() 时,
时,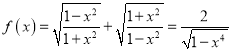
![]() 时
时![]() 最小值为2.
最小值为2.
(2)![]() 时,
时,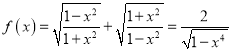
![]() 时,
时,![]() 递增;
递增;![]() 时,
时,![]() 递减;
递减;
![]() 为偶函数.所以只对
为偶函数.所以只对![]() 时,说明
时,说明![]() 递增.
递增.
设![]() ,所以
,所以![]() ,得
,得![]()
![]()
所以![]() 时,
时,![]() 递增;
递增;
(3)![]() ,
,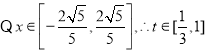 ,
,![]()
从而原问题等价于求实数![]() 的范围,使得在区间
的范围,使得在区间![]() 上,
上,
恒有![]() .
.
①当![]() 时,
时,![]() 在
在![]() 上单调递增,
上单调递增,
![]() 由
由![]() 得
得![]() ,
,
从而![]() ;
;
②当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
由![]() 得
得![]() ,从而
,从而![]() ;
;
③当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
![]() ,
,
由![]() 得
得![]() ,从而
,从而![]() ;
;
④当![]() 时,
时,![]() 在
在![]() 上单调递减,
上单调递减,
![]()
由![]() 得
得![]() ,从而
,从而![]() ;
;
综上,![]() .
.

【题目】某企业为打入国际市场,决定从![]() 、
、![]() 两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
两种产品中只选择一种进行投资生产,已知投资生产这两种产品的有关数据如下表:(单位:万美元)
年固定成本 | 每件产品成本 | 每件产品销售价 | 每年最多可生产的件数 | |
A产品 | 20 |
| 10 | 200 |
B产品 | 40 | 8 | 18 | 120 |
其中年固定成本与年生产的件数无关,![]() 是待定常数,其值由生产
是待定常数,其值由生产![]() 产品的原材料决定,预计
产品的原材料决定,预计![]() ,另外,年销售
,另外,年销售![]() 件B产品时需上交
件B产品时需上交![]() 万美元的特别关税,假设生产出来的产品都能在当年销售出去.
万美元的特别关税,假设生产出来的产品都能在当年销售出去.
(1)求该厂分别投资生产A、![]() 两种产品的年利润
两种产品的年利润![]() 与生产相应产品的件数
与生产相应产品的件数![]() 之间的函数关系,并求出其定义域;
之间的函数关系,并求出其定义域;
(2)如何投资才可获得最大年利润?请设计相关方案.
【题目】某中学为了解高一年级学生身高发育情况,对全校![]() 名高一年级学生按性别进行分层抽样检查,测得身高(单位:
名高一年级学生按性别进行分层抽样检查,测得身高(单位:![]() )频数分布表如表
)频数分布表如表![]() 、表
、表![]() .
.
表![]() :男生身高频数分布表
:男生身高频数分布表
身高/ |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
表![]() :女生身高频数分布表
:女生身高频数分布表
身高/ |
|
|
|
|
|
|
频数 |
|
|
|
|
|
|
(1)求该校高一女生的人数;
(2)估计该校学生身高在![]() 的概率;
的概率;
(3)以样本频率为概率,现从高一年级的男生和女生中分别选出![]() 人,设
人,设![]() 表示身高在
表示身高在![]() 学生的人数,求
学生的人数,求![]() 的分布列及数学期望.
的分布列及数学期望.