��Ŀ����
����Ŀ��ij��ҵΪ��������г���������![]() ��
��![]() ���ֲ�Ʒ��ֻѡ��һ�ֽ���Ͷ����������֪Ͷ�����������ֲ�Ʒ���й��������±���(��λ������Ԫ)
���ֲ�Ʒ��ֻѡ��һ�ֽ���Ͷ����������֪Ͷ�����������ֲ�Ʒ���й��������±���(��λ������Ԫ)
��̶��ɱ� | ÿ����Ʒ�ɱ� | ÿ����Ʒ���ۼ� | ÿ�����������ļ��� | |
A��Ʒ | 20 |
| 10 | 200 |
B��Ʒ | 40 | 8 | 18 | 120 |
������̶��ɱ����������ļ����أ�![]() �Ǵ�����������ֵ������
�Ǵ�����������ֵ������![]() ��Ʒ��ԭ���Ͼ�����Ԥ��
��Ʒ��ԭ���Ͼ�����Ԥ��![]() �����⣬������
�����⣬������![]() ��B��Ʒʱ���Ͻ�
��B��Ʒʱ���Ͻ�![]() ����Ԫ���ر��˰���������������IJ�Ʒ�����ڵ������۳�ȥ��
����Ԫ���ر��˰���������������IJ�Ʒ�����ڵ������۳�ȥ��
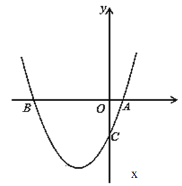
��1����ó��ֱ�Ͷ������A��![]() ���ֲ�Ʒ��������
���ֲ�Ʒ��������![]() ��������Ӧ��Ʒ�ļ���
��������Ӧ��Ʒ�ļ���![]() ֮��ĺ�����ϵ��������䶨����
֮��ĺ�����ϵ��������䶨����
��2�����Ͷ�ʲſɻ������������������ط�����
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() ����2����
����2����![]() ʱ��Ͷ������
ʱ��Ͷ������![]() ��Ʒ
��Ʒ![]() ���ɻ���������������
���ɻ���������������![]() ʱ������
ʱ������![]() ��Ʒ������
��Ʒ������![]() ��Ʒ���ɻ���������������
��Ʒ���ɻ���������������![]() ʱ��Ͷ������
ʱ��Ͷ������![]() ��Ʒ
��Ʒ![]() ���ɻ�����������.
���ɻ�����������.
��������
�����������1��������֪������![]() ��Ʒ��������
��Ʒ��������![]() �����ܶ�
�����ܶ�![]() �����ɱ�������
�����ɱ�������![]() ��Ʒ��������
��Ʒ��������![]() �����ܶ�
�����ܶ�![]() �����ɱ�
�����ɱ�![]() �Ͻ���˰���������ݱ������
�Ͻ���˰���������ݱ������![]() �Ľ���ʽ����ȷ������
�Ľ���ʽ����ȷ������![]() ��ȡֵ��Χ����2���ɣ�1����֪��������һ�κ����ĵ����ԡ����κ�������ֵ���ֱ������������
��ȡֵ��Χ����2���ɣ�1����֪��������һ�κ����ĵ����ԡ����κ�������ֵ���ֱ������������![]() �����ֵ�����ò����
�����ֵ�����ò����![]() �����ֵ�Ĵ�С���бȽϣ����Բ���
�����ֵ�Ĵ�С���бȽϣ����Բ���![]() �ķ�Χ���м��ۣ��Ӷ�����ɵý�.
�ķ�Χ���м��ۣ��Ӷ�����ɵý�.
�����������1������������Ϊ![]() ����������ļ��㹫ʽ��������A��B����Ʒ��������
����������ļ��㹫ʽ��������A��B����Ʒ��������![]() �ֱ�Ϊ��
�ֱ�Ϊ��
![]() ������3��
������3��
![]()
![]()
![]() ��
��![]() ��
��![]() ����5��
����5��
��2��![]()
![]() ��
��![]()
![]() ��
��![]()
![]() ��������
��������
��![]() ��
��![]() ��
��![]()
![]() ʱ������A��Ʒ���������Ϊ
ʱ������A��Ʒ���������Ϊ
![]() ������Ԫ��������������7��
������Ԫ��������������7��
��![]() ��
��![]() ��
��![]() ��
��![]()
![]() ʱ��
ʱ��
����B��Ʒ���������Ϊ460��������������������9��
����Ƚϣ�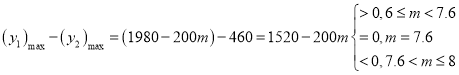
���ԣ���![]() ʱ��Ͷ������A��Ʒ200���ɻ�����������
ʱ��Ͷ������A��Ʒ200���ɻ�����������
��![]() ʱ������A��Ʒ������B��Ʒ���ɻ�����������
ʱ������A��Ʒ������B��Ʒ���ɻ�����������
��![]() ʱ��Ͷ������B��Ʒ100���ɻ�����������. ������������12��
ʱ��Ͷ������B��Ʒ100���ɻ�����������. ������������12��

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ���ռ�����֪ʶ��ǿ������ʶ��ijУ��������רҵ�װ��ȡ60�ˣ�����ʷ���Ұ��ȡ50�˲μӻ���֪ʶ���ԣ�
��1��������Ŀ�����������2��2�����������ݴ��ж����Ƿ���99%�İ�����Ϊ����֪ʶ��רҵ�й���
���� | ������ | �ܼ� | |
�װ� | |||
�Ұ� | 30 | ||
�ܼ� | 60 |
��2��Ϊ�μ��ϼ��ٰ�Ļ���֪ʶ������ѧУ�ٰ�Ԥѡ����Ԥѡ���������100�֣�������ͬѧ��60������ͨ��Ԥѡ����������ͬѧ��80������ͨ��Ԥѡ����ÿλͬѧ��60�����ϵĸ���Ϊ![]()
![]() ����80�����ϵĸ���Ϊ
����80�����ϵĸ���Ϊ![]() ������֪�װ���3�˲μ�Ԥѡ��������1��Ϊ����ѧ�������������X��ʾ�װ�ͨ��Ԥѡ��������
������֪�װ���3�˲μ�Ԥѡ��������1��Ϊ����ѧ�������������X��ʾ�װ�ͨ��Ԥѡ��������
��X�ķֲ��м�����E��X��.
��: ![]() , n=a+b+c+d
, n=a+b+c+d
P(K2>k0) | 0.100 | 0.050 | 0.025 | 0.010[ | 0.005 |
k0 | 2.706 | 3.84 | 5.02 | 6.635 | 7.879 |
����Ŀ��ijũ�����Զ�����ҹ�²��С��ij�����ڴ���Ʒ�ַ�ѿ����֮��Ĺ�ϵ���з����о������Ƿֱ��¼��12��1����12��5����ÿ����ҹ�²���ʵ����ÿ��ÿ100�������еķ�ѿ�����õ��������ϣ�
�� �� | 12��1�� | 12��2�� | 12��3�� | 12��4�� | 12��5�� |
�²�x����C�� | 10 | 11 | 13 | 12 | 8 |
��ѿ��y������ | 23 | 25 | 30 | 26 | 16 |
��1�������12��2����12��4�������ݣ����y����x�����Իع鷽��![]() �������������
�������������![]() ����
����
��2���������Իع鷽�̵õ��Ĺ�����������ѡ���ļ���������ѡȡ������������12��1����12��5��������������������������2�ţ�����Ϊ�õ������Իع鷽���ǿɿ��ģ�������2�������õ����Իع鷽���Ƿ�ɿ���