题目内容

（2012•台州模拟）设变量x、y满足约束条件：
x≥2
y≤x+1
y≥2x-3
，则目标函数z=2x+3y的最大值为
23
23
．
分析：确定不等式表示的平面区域，明确目标函数的几何意义，即可求得最大值．
解答：解：不等式表示的平面区域如图所示

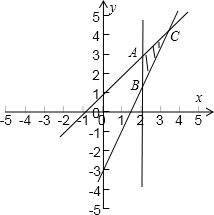
目标函数z=2x+3y，即y=-
2
3
x+
z
3
，则直线过点C时，纵截距最大，
此时，由
y=x+1
y=2x-3
，可得x=4，y=5
∴目标函数z=2x+3y的最大值为2×4+3×5=23
故答案为：23
点评：本题考查线性规划知识，考查数形结合的数学思想，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
（2012•台州模拟）已知函数f（x）=lnx-
1
2
ax2-2x（a＜0）
（Ⅰ）若函数f（x）存在单调递减区间，求a的取值范围；
（Ⅱ）若a=-
1
2
且关于x的方程f（x）=-
1
2
x+b在[1，4]上恰有两个不相等的实数根，求实数b的取值范围．
（2012•台州模拟）在平面直角坐标系中，定义d（P，Q）=|x1-x2|+|y1-y2|为两点P（x1，y1），Q（x2，y2）之间的“折线距离”．则原点O（0，0）与直线2x+y-
5
=0上一点P（x，y）的“折线距离”的最小值是
5
2
5
2
．
（2012•台州模拟）已知函数f（x）=log2（ax2+2x-3a）．
（Ⅰ）当a=-1时，求该函数的定义域和值域；
（Ⅱ）如果f（x）≥1在区间[2，3]上恒成立，求实数a的取值范围．
（2012•台州模拟）在边长为6的等边△ABC中，点M满足
BM
=2
MA
，则
CM
•
CB
等于
24
24
．
（2012•台州模拟）设|
a
|=|
b
|=|
a
+
b
|≠0，那么
a
-
b
与
b
的夹角为（　　）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网