题目内容
(2012•台州模拟)在平面直角坐标系中,定义d(P,Q)=|x1-x2|+|y1-y2|为两点P(x1,y1),Q(x2,y2)之间的“折线距离”.则原点O(0,0)与直线2x+y-
=0上一点P(x,y)的“折线距离”的最小值是
.
| 5 |
| ||
| 2 |
| ||
| 2 |
分析:根据新定义直接求出d(A,O);求出过O与直线 2x+y-
=0的点坐标的“折线距离”的表达式,然后求出最小值.
| 5 |
解答: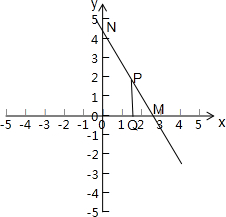 解:如图,直线与两轴的交点分别为 N(0,
解:如图,直线与两轴的交点分别为 N(0,
),M(
,0),
设P(x,y)为直线上任意一点,作PQ⊥x轴于Q,于是有|PQ|=2|QM|,
所以d=|OQ|+|QP|≥|OQ|+|QM|≥|OM|,即当P与M重合时,dmin=|OM|=
.
故答案为:
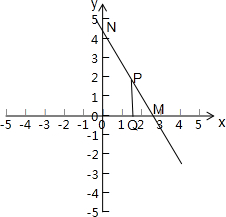 解:如图,直线与两轴的交点分别为 N(0,
解:如图,直线与两轴的交点分别为 N(0,| 5 |
| ||
| 2 |
设P(x,y)为直线上任意一点,作PQ⊥x轴于Q,于是有|PQ|=2|QM|,
所以d=|OQ|+|QP|≥|OQ|+|QM|≥|OM|,即当P与M重合时,dmin=|OM|=
| ||
| 2 |
故答案为:
| ||
| 2 |
点评:本题是中档题,考查新定义,利用新定义求出函数的最小值问题,考查计算能力,对新定义的理解和灵活运应是解好本题的关键.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目