题目内容
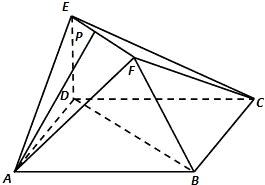 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和
直角梯形BDEF所在的平面互相垂直,EF∥BD,
ED⊥BD,AD= ,EF=ED=1,点P为线段
,EF=ED=1,点P为线段
EF上任意一点.
(Ⅰ)求证:CF⊥AP;
(Ⅱ)求二面角B-AF-E的余弦值.
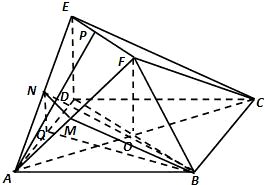 解:(Ⅰ)∵平面BDEF⊥平面ABCD,ED⊥BD,
解:(Ⅰ)∵平面BDEF⊥平面ABCD,ED⊥BD,∴ED⊥平面ABCD
连接AC交BD于点O,连接FO,
∵正方形ABCD的边长为
 ,∴AC=BD=2;
,∴AC=BD=2;在直角梯形BDEF中,∵EF=ED=1,
O为BD中点,∴FO∥ED,且FO=1;
易求得AF=CF=
 ,AE=CE=
,AE=CE= ,
,由勾股定理知CF⊥EF,AF⊥EF
由AF=CF=
 ,AC=2可知CF⊥AF.EF∩AF=F,∴CF⊥平面AEF
,AC=2可知CF⊥AF.EF∩AF=F,∴CF⊥平面AEF∵点P为线段EF上任意一点,∴AP?平面AEF∴CF⊥AP
(Ⅱ)取AF中点M,AE中点N,连接BM、MN、BN,
∵AB=AF=BF=
 ,∴BM⊥AF,又MN∥EF,AF⊥EF∴MN⊥AF
,∴BM⊥AF,又MN∥EF,AF⊥EF∴MN⊥AF∴∠BMN是二面角B-AF-E的平面角.
易求得BM=
 AB=
AB= ,MN=
,MN= EF=
EF= ,设AD中点为Q,则NQ∥ED,
,设AD中点为Q,则NQ∥ED,NQ⊥BQ,可求得BN2=NQ2+BQ2=
 ,
,在△BMN中,由余弦定理求得,cos∠BMN=-

二面角B-AF-E的余弦值为-

分析:(I)由题意平面BDEF⊥平面ABCD,ED⊥BD,得ED⊥平面ABCD,在利用所给的边长关系得到线线垂直,进而得到线面垂直,再有线面垂直得出线线垂直即可;
(II)由题意及所给图形利用(I)的证明过程及二面角的概念可以找到二面角的平面角,然后再在三角形中解出.
点评:(I)此问重点考查了利用面面垂直得到线面垂直,在有线线垂直得到线面垂直,有线面垂直得出线线垂直.这三者的相互转化;
(II)此问重点考查了二面角的平面角的概念及利用定义求其二面角的方法,还考查了利用余弦定理解三角形.

练习册系列答案
相关题目
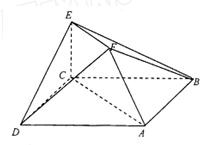 在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=
在如图所示的多面体中,已知正方形ABCD和直角梯形ACEF所在的平面互相垂直,EC⊥AC,EF∥AC,AB=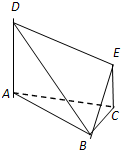 在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.
在如图所示的多面体中,底面△ABC是边长为2的正三角形,DA和EC均垂直于平面ABC,且DA=2,EC=1.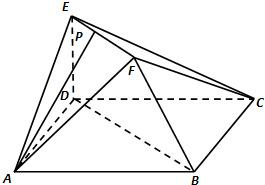 在如图所示的多面体中,已知正方形ABCD和
在如图所示的多面体中,已知正方形ABCD和 (2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点.
(2012•日照一模)在如图所示的多面体中,EF⊥平面AEB,AE⊥EB,AD∥EF,EF∥BC,BC=2AD=4,EF=3,AE=BE=2,G是BC的中点. 在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.
在如图所示的多面体中,AA1∥BB1,CC1⊥AC,CC1⊥BC.