题目内容
如图,四棱锥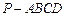 的底面
的底面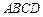 为一直角梯形,其中
为一直角梯形,其中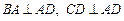 ,
,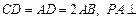 底面
底面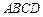 ,
,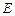 是
是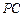 的中点.
的中点.
(1)试用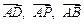 表示
表示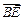 ,并判断直线
,并判断直线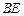 与平面
与平面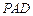 的位置关系;
的位置关系;
(2)若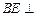 平面
平面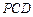 ,求异面直线
,求异面直线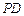 与
与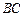 所成角的余弦值.
所成角的余弦值.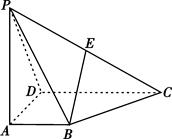
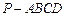 的底面
的底面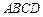 为一直角梯形,其中
为一直角梯形,其中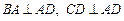 ,
,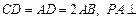 底面
底面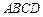 ,
,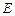 是
是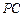 的中点.
的中点.(1)试用
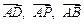 表示
表示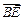 ,并判断直线
,并判断直线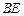 与平面
与平面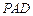 的位置关系;
的位置关系;(2)若
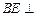 平面
平面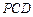 ,求异面直线
,求异面直线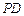 与
与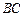 所成角的余弦值.
所成角的余弦值.
解:设 ,建立如图所示空间直角坐标系,
,建立如图所示空间直角坐标系,
 ,
, ,
,
 ,
, . ……(2分)
. ……(2分)
(1) ,
, ,
,
所以 , ……(5分)
, ……(5分)
 平面
平面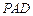 ,
, 平面
平面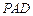 . ……(7分)
. ……(7分)
(2) 平面
平面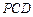 ,
, ,即
,即 .
.
 ,
, ,即
,即 . ……(10分)
. ……(10分)
 , ……(11分)
, ……(11分)
 ,
,
所以异面直线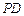 与
与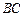 所成角的余弦值为
所成角的余弦值为 . ……(14分)
. ……(14分)
 ,建立如图所示空间直角坐标系,
,建立如图所示空间直角坐标系, ,
, ,
, ,
, . ……(2分)
. ……(2分)(1)
 ,
, ,
,所以
 , ……(5分)
, ……(5分) 平面
平面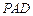 ,
, 平面
平面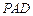 . ……(7分)
. ……(7分)(2)
 平面
平面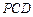 ,
, ,即
,即 .
. ,
, ,即
,即 . ……(10分)
. ……(10分) , ……(11分)
, ……(11分) ,
,所以异面直线
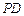 与
与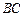 所成角的余弦值为
所成角的余弦值为 . ……(14分)
. ……(14分)略

练习册系列答案
相关题目
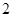 的正方体
的正方体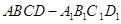 中,
中,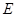 、
、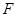 分别是
分别是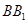 、
、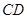 的中点,试用向量的方法:
的中点,试用向量的方法: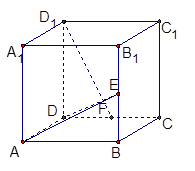
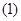 求证:
求证: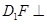 平面
平面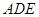 ;
;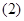 求
求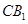 与平面
与平面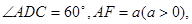 (I)求证:AC⊥BF;
(I)求证:AC⊥BF;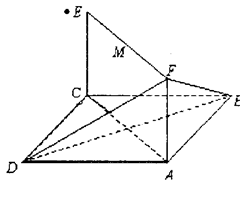
 B
B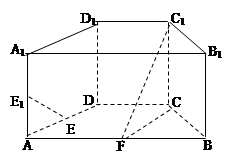
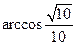 ,求BD的长度.(15分)
,求BD的长度.(15分)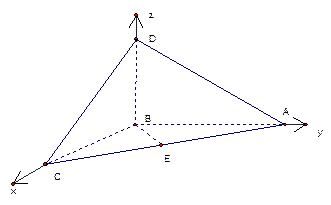
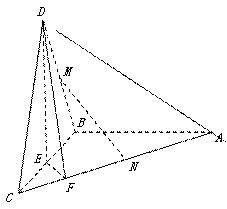

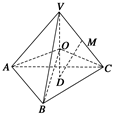
 中,
中,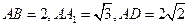 ,
, 为
为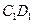 的中点,
的中点,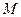 为
为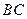 的中点。
的中点。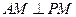 ;
;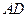 与平面
与平面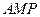 所成角的正弦值。
所成角的正弦值。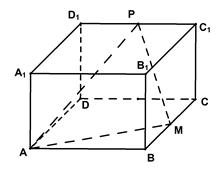
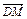 ,
,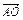 〉.
〉.