题目内容
(本题满分16分)(Ⅰ)试比较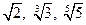 的大小;
的大小;
(Ⅱ)试比较nn+1与(n+1)n(n∈N+)的大小,根据(Ⅰ)的结果猜测一个一般性结论,并加以证明.
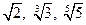 的大小;
的大小;(Ⅱ)试比较nn+1与(n+1)n(n∈N+)的大小,根据(Ⅰ)的结果猜测一个一般性结论,并加以证明.
解:(Ⅰ)由于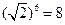 ,
,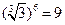 ,则
,则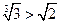 ;
;
又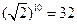 ,
,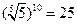 ,则
,则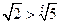 ;
;
所以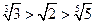 . …………………………………………6分
. …………………………………………6分
(Ⅱ)当n=1,2时,有nn+1<(n+1)n.………………………………………8分
当n≥3时,有nn+!>(n+1)n. 证明如下:
令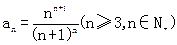 ,
,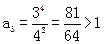 .
.
又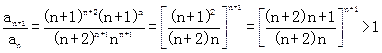 .
.
∴an+1>an即数列{an}是一个单调递增数列.
则an>an-1>…>a3>1
∴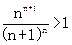 即nn+1>(n+1)n. ……………………………………16分
即nn+1>(n+1)n. ……………………………………16分
另证:构造函数f(x)=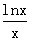 (x≥3),f
(x≥3),f (x)=
(x)=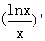 =
=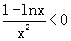 ,
,
∴f(x)=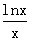 在[3,+∞
在[3,+∞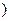 为递减函数,则f(n)>f(n+1),
为递减函数,则f(n)>f(n+1),
即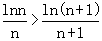 ,
,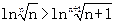 ,∴
,∴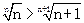 ,
,
即nn+1>(n+1 )n(n≥3时结论成立).
)n(n≥3时结论成立).
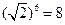 ,
,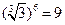 ,则
,则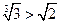 ;
;又
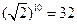 ,
,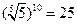 ,则
,则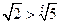 ;
;所以
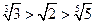 . …………………………………………6分
. …………………………………………6分(Ⅱ)当n=1,2时,有nn+1<(n+1)n.………………………………………8分
当n≥3时,有nn+!>(n+1)n. 证明如下:
令
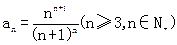 ,
,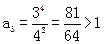 .
. 又
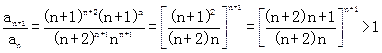 .
. ∴an+1>an即数列{an}是一个单调递增数列.
则an>an-1>…>a3>1
∴
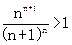 即nn+1>(n+1)n. ……………………………………16分
即nn+1>(n+1)n. ……………………………………16分另证:构造函数f(x)=
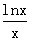 (x≥3),f
(x≥3),f (x)=
(x)=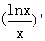 =
=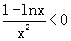 ,
,∴f(x)=
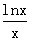 在[3,+∞
在[3,+∞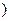 为递减函数,则f(n)>f(n+1),
为递减函数,则f(n)>f(n+1),即
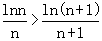 ,
,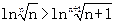 ,∴
,∴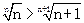 ,
,即nn+1>(n+1
 )n(n≥3时结论成立).
)n(n≥3时结论成立).略

练习册系列答案
相关题目

 (
(
 )则
)则 2+
2+ 的最大值是( )
的最大值是( ) ,且
,且 则
则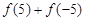 的值为( )
的值为( )

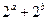 的最小值为
的最小值为 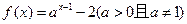 图象恒过定点
图象恒过定点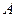 ,且点
,且点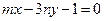 上,则
上,则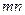 的取值范围为
的取值范围为 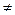 1,函数f(x)=alg(x2-2a+1)有最小值,则不等式loga(x2-5x+7)>0的解集为___________
1,函数f(x)=alg(x2-2a+1)有最小值,则不等式loga(x2-5x+7)>0的解集为___________ 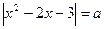 有两个实数根,则
有两个实数根,则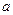 的取值范围是
的取值范围是 
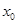 是方程式
是方程式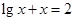 的解,则
的解,则