题目内容
【题目】平面直角坐标系中有16个格点(i,j),其中0≤i≤3,0≤j≤3.若在这16个点中任取n个点,这n个点中总存在4个点,这4个点是一个正方形的顶点,求n的最小值.
【答案】11.
【解析】
分两步来证明:先找到10个点,它们中的任意四点不能构成正方形的顶点,再根据抽屉原理证明任意的11个点,一定存在4个点为正方形的四个顶点.
存在下面的10点即:
点(0,0),(1,0),(2,0),(2,1),(3,1),(0,2),(3,2),(0,3),(1,3),(3,3),
其中任意4个点不能构成正方形的顶点,故![]() .
.
下证:任意11点中,一定存在4个点为正方形的四个顶点.
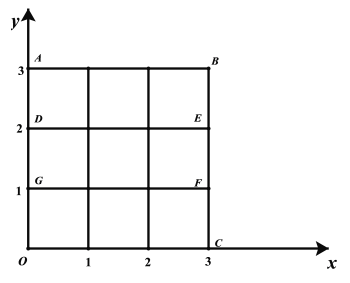
因为共取11个点,分两种情况讨论:
(1)有一行有4个点(设为![]() ),则余下三行共有7个点,
),则余下三行共有7个点,
由抽屉原理知余下三行中必有一行至少有3个点(设为![]() ),
),
因![]() ,
,![]() 分布在两行,
分布在两行,
若该两行相邻或中间隔一行,则存在四个点,它们为正方形的四个顶点;
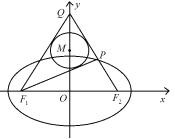
若该两行间隔两行,如图,不妨设![]() 为线段
为线段![]() 上的格点,
上的格点,![]() 为线段
为线段![]() 上的格点,对应的点的坐标为
上的格点,对应的点的坐标为![]() ,
,
余下4个点分布在中间两行,若线段![]() 上有两个整点,则它们和
上有两个整点,则它们和![]() 中的两点构成正方形的顶点,否则线段
中的两点构成正方形的顶点,否则线段![]() 上至少有3个点,则其中必有两个格点与
上至少有3个点,则其中必有两个格点与![]() 中的两点构成正方形的顶点.
中的两点构成正方形的顶点.
(2)任意一行都没有4个点,则各行的格点数分别为![]() ,故4行中必有相邻两行各有3个格点,这6个格点中必存在4个格点,它们构成正方形的顶点.
,故4行中必有相邻两行各有3个格点,这6个格点中必存在4个格点,它们构成正方形的顶点.

【题目】下表是某原料在市场上从2013年至2019年这7年中每年的平均价格(单位:千元/吨)数据:
年份 | 2013 | 2014 | 2015 | 2016 | 2017 | 2018 | 2019 |
年份代号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
平均价格 (单位:千元/吨) |
|
|
|
|
|
|
|
(![]() 和
和![]() 线性相关性较强,求出以
线性相关性较强,求出以![]() 为解释变量
为解释变量![]() 为预报变量的线性回归方程(系数精确到
为预报变量的线性回归方程(系数精确到![]() );
);
(2)以(1)的结论为依据,预测2032年该原料价格.预估该原料价格在哪一年突破1万元/吨?
参考数据:![]() ,
,![]() ,
,![]() ,
,![]()
参考公式:回归方程![]() 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: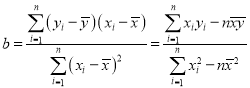 ,
,![]() .
.