题目内容
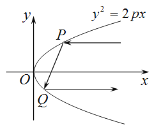
【题目】抛物线有如下光学性质:由其焦点射出的光线经抛物线反射后,沿平行于抛物线对称轴的方向射出.现有抛物线![]() ,如图一平行于
,如图一平行于![]() 轴的光线射向抛物线,经两次反射后沿平行
轴的光线射向抛物线,经两次反射后沿平行![]() 轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
轴方向射出,若两平行光线间的最小距离为4,则该抛物线的方程为__________.
【答案】![]()
【解析】
先由题意得到![]() 必过抛物线的焦点,设出直线
必过抛物线的焦点,设出直线![]() 的方程,联立直线
的方程,联立直线![]() 与抛物线方程,表示出弦长,再根据两平行线间的最小距离时,
与抛物线方程,表示出弦长,再根据两平行线间的最小距离时,![]() 最短,进而可得出结果.
最短,进而可得出结果.
由抛物线的光学性质可得:![]() 必过抛物线的焦点
必过抛物线的焦点![]() ,
,
当直线![]() 斜率存在时,设
斜率存在时,设![]() 的方程为
的方程为![]() ,
,![]() ,
,
由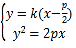 得:
得:![]() ,整理得
,整理得![]() ,
,
所以![]() ,
,![]() ,
,
所以![]() ;
;
当直线![]() 斜率不存在时,易得
斜率不存在时,易得![]() ;
;
综上,当直线![]() 与
与![]() 轴垂直时,弦长最短,
轴垂直时,弦长最短,
又因为两平行光线间的最小距离为4,![]() 最小时,两平行线间的距离最小;
最小时,两平行线间的距离最小;
因此![]() ,所求方程为
,所求方程为![]() .
.
故答案为![]()

练习册系列答案
相关题目