题目内容

设S1={
ab
cd
|a，b，c，d∈R， b=c}，S2={
ab
cd
|a，b，c，d∈R， a=d=b+c=0}．
已知矩阵
24
68
=A+B，其中A∈S1，B∈S2．那么A-B=
 
．
分析：利用A∈S1，B∈S2．设A= 
ab
bd
，B= 
0-c
c0
求出A+B，结合已知矩阵
24
68
=A+B，列出关于a，b，c，d的方程组，求出a，b，c，d．即可得到B，从而解决问题．
解答：解：∵A∈S1，B∈S2．
∴设A= 
ab
bd
，B= 
0-c
c0

∴A+B=
ab-c
b+cd

已知矩阵
24
68
=A+B，
∴
a=2
b-c=4
b+c=6
d=8

∴
a=2
b=5
c=1
d=8
那么B=〔
0-1
10
〕
那么A-B=
25
58
-
0-1
10
=〔
26
48
〕
故答案为：〔
26
48
〕．
点评：本小题主要考查二阶矩阵、方程组的解法等基础知识，考查待定系数法思想．属于基础题．
练习册系列答案
相关题目
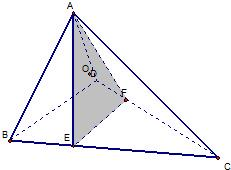11、如图，在四面体ABCD中，截面AEF经过四面体的内切球（与四个面都相切的球）球心O，且与BC，DC分别截于E、F，如果截面将四面体分成体积相等的两部分，设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1，S2，则必有（　　）
如图，在梯形ABCD中，AB∥CD，AB=a，CD=b（a＞b）．若EF∥AB，EF到CD与AB的距离之比为m：n，则可推算出：EF=
ma+nb
m+n
，用类比的方法，推想出下列问题的结果，在上面的梯形ABCD中，延长梯形的两腰AD和BC交于O点，设△OAB，△OCD的面积分别为S1，S2，EF∥AB，，且EF到CD与AB的距离之比为m：n，则△OEF的面积S0与S1，S2的关系是（　　）
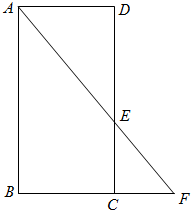矩形ABCD中，AB=2，BC=1，E为CD上一点，且DE=x，延长AE交BC延长线于点F，设△CEF，△ADE的面积分别为S1，S2令S=S1+S2．
（Ⅰ）求S关于x的解析式；
（Ⅱ）求S的最小值．
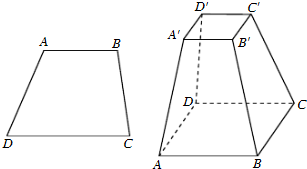（必做题）先阅读：如图，设梯形ABCD的上、下底边的长分别是a，b（a＜b），高为h，求梯形的面积．
方法一：延长DA、CB交于点O，过点O作CD的垂线分别交AB、CD于E、F，则EF=h．
设OE=x，∵△OAB∽△ODC，∴
x
x+h
=
a
b
，即x=
ah
b-a
．
∴S梯形ABCD=S△ODC-S△OAB=
1
2
b（x+h）-
1
2
ax=
1
2
（b-a）x+
1
2
bh=
1
2
（a+b）h．
方法二：作AB的平行线MN分别交AD、BC于MN，过点A作BC的平行线AQ分别于MN、DC于PQ，则△AMP∽△ADQ．
设梯形AMNB的高为x，MN=y，
x
h
=
y-a
b-a
⇒y=a+
b-a
h
x，∴S梯形ABCD=
∫
h
0
（a+
b-a
h
x）dx=（ax+
b-a
2h
x2）
|
h
0
=ah+
b-a
2h
•h2=
1
2
（a+b）h．
再解下面的问题：
已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1，S2（S1＜S2），棱台的高为h，类比以上两种方法，分别求出棱台的体积（棱锥的体积=
1
3
×底面积×高）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网