题目内容
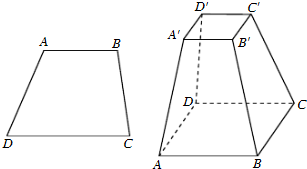 (必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.
(必做题)先阅读:如图,设梯形ABCD的上、下底边的长分别是a,b(a<b),高为h,求梯形的面积.方法一:延长DA、CB交于点O,过点O作CD的垂线分别交AB、CD于E、F,则EF=h.
设OE=x,∵△OAB∽△ODC,∴
| x |
| x+h |
| a |
| b |
| ah |
| b-a |
∴S梯形ABCD=S△ODC-S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
方法二:作AB的平行线MN分别交AD、BC于MN,过点A作BC的平行线AQ分别于MN、DC于PQ,则△AMP∽△ADQ.
设梯形AMNB的高为x,MN=y,
| x |
| h |
| y-a |
| b-a |
| b-a |
| h |
| ∫ | h 0 |
| b-a |
| h |
| b-a |
| 2h |
| | | h 0 |
| b-a |
| 2h |
| 1 |
| 2 |
再解下面的问题:
已知四棱台ABCD-A′B′C′D′的上、下底面的面积分别是S1,S2(S1<S2),棱台的高为h,类比以上两种方法,分别求出棱台的体积(棱锥的体积=
| 1 |
| 3 |
分析:在平面几何中的进行几何性质类比推理时,我们常用的思路是:由平面几何中线段的性质,类比推理平面几何中面积的性质,再结合已知的梯形的面积的步骤,即可类比得到棱台的体积.
解答:解:法一:将V四棱台ABCD-A′B′C′D′补为四棱锥V-ABCD,
设点V到面A′B′C′D′的距离为h′,面ABCD与面A′B′C′D′的距离为棱台的高h,
∵四边形ABCD∽四边形A′B′C′D′,上、下底面的面积分别是S1,S2,
∴
=
,∴h′=
;
∴V四棱台ABCD-A′B′C′D′=V四棱锥A′B′C′D′-V四棱锥ABCD
=
×S2×(h+h′)-
×S1×h′=
S2h+
(S2-S1)h′=
(S1+
+S2)h.
所以,四棱台ABCD-A′B′C′D′的体积为
(S1+
+S2)h.
法二:作一与上下底面平行的平面A″B″C″D″截得四边形的面积为S,它与上底面的距离为x,
过棱A′D′作B′C′CB的平行于平面A′D′PQ,与A″B″、C″D″、AB、CD分别交于M、N、P、Q,
则△AMN∽△APQ,∴
=
,∴S=S1+
(S2-S1),
∴V四棱台ABCD-A′B′C′D′=
[S1+
(S2-S1)]dx
=[S1x+
(S2-S1)]
=
(S1+
+S2)h.
∴四棱台ABCD-A′B′C′D′的体积为为
(S1+
+S2)h.
设点V到面A′B′C′D′的距离为h′,面ABCD与面A′B′C′D′的距离为棱台的高h,
∵四边形ABCD∽四边形A′B′C′D′,上、下底面的面积分别是S1,S2,
∴
| s1 |
| s2 |
| h′2 |
| (h+h′)2 |
h
| ||||
|
∴V四棱台ABCD-A′B′C′D′=V四棱锥A′B′C′D′-V四棱锥ABCD
=
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 3 |
| S1S2 |
所以,四棱台ABCD-A′B′C′D′的体积为
| 1 |
| 3 |
| S1S2 |
法二:作一与上下底面平行的平面A″B″C″D″截得四边形的面积为S,它与上底面的距离为x,
过棱A′D′作B′C′CB的平行于平面A′D′PQ,与A″B″、C″D″、AB、CD分别交于M、N、P、Q,
则△AMN∽△APQ,∴
| x2 |
| h2 |
| S-S1 |
| S2-S1 |
| x2 |
| h2 |
∴V四棱台ABCD-A′B′C′D′=
| ∫ | h 0 |
| x2 |
| h2 |
=[S1x+
| 1 |
| 3 |
| x3 |
| h2 |
| | | h 0 |
| 1 |
| 3 |
| S1S2 |
∴四棱台ABCD-A′B′C′D′的体积为为
| 1 |
| 3 |
| S1S2 |
点评:本题考查的知识点是类比推理,类比推理的一般步骤是:(1)找出两类事物之间的相似性或一致性;(2)用一类事物的性质去推测另一类事物的性质,得出一个明确的命题(猜想).

练习册系列答案
相关题目