题目内容
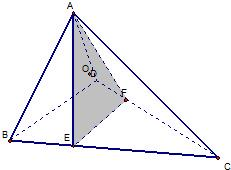 11、如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有( )
11、如图,在四面体ABCD中,截面AEF经过四面体的内切球(与四个面都相切的球)球心O,且与BC,DC分别截于E、F,如果截面将四面体分成体积相等的两部分,设四棱锥A-BEFD与三棱锥A-EFC的表面积分别是S1,S2,则必有( )分析:比较表面积的大小,可以通过体积进行转化比较;也可以先求表面积,然后比较.
解答:解:连OA、OB、OC、OD,
则VA-BEFD=VO-ABD+VO-ABE+VO-BEFD
VA-EFC=VO-ADC+VO-AEC+VO-EFC
又VA-BEFD=VA-EFC
而每个三棱锥的高都是原四面体的内切球的半径,又面AEF公共,
故SABD+SABE+SBEFD=SADC+SAEC+SEFC
故选C
则VA-BEFD=VO-ABD+VO-ABE+VO-BEFD
VA-EFC=VO-ADC+VO-AEC+VO-EFC
又VA-BEFD=VA-EFC
而每个三棱锥的高都是原四面体的内切球的半径,又面AEF公共,
故SABD+SABE+SBEFD=SADC+SAEC+SEFC
故选C
点评:本题考查球的内接体的表面积问题,找出表面积的共有特征是解题简化的关键,是中档题.

练习册系列答案
相关题目
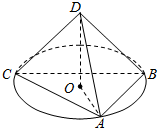 如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )
如图,在四面体ABCD中,DA=DB=DC=1,且DA,DB,DC两两互相垂直,点O是△ABC的中心,将△DAO绕直线DO旋转一周,则在旋转过程中,直线DA与BC所成角的余弦值的取值范围是( )A、[0,
| ||||
B、[0,
| ||||
C、[0,
| ||||
D、[0,
|
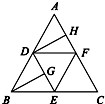 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为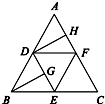 如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )
如图,在正三角形ABC中,D,E,F分别为各边的中点,G,H分别为DE,AF的中点,将△ABC沿DE,EF,DF折成正四面体P-DEF,则四面体中异面直线PG与DH所成的角的余弦值为( )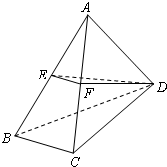 如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.
如图,在四面体ABCD中,BC⊥面ACD,DA=DC,E、F分别为AB、AC的中点.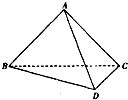 (2009•武汉模拟)如图,在四面体A-BCD中,
(2009•武汉模拟)如图,在四面体A-BCD中,