题目内容
已知函数 和
和 都是定义在R上的偶函数,若
都是定义在R上的偶函数,若 时,
时, ,则
,则 为( )
为( )
| A.正数 | B.负数 | C.零 | D.不能确定 |
A
解析试题分析:∵函数 是偶函数,∴
是偶函数,∴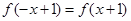 .又函数
.又函数 也是偶函数,∴函数
也是偶函数,∴函数 既关于直线
既关于直线 对称,又关于y轴对称,所以函数
对称,又关于y轴对称,所以函数 是周期为2的周期函数,故有
是周期为2的周期函数,故有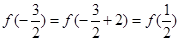 ,
,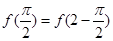 .又当
.又当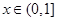 时,
时,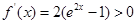 恒成立,故函数
恒成立,故函数 为增函数.又
为增函数.又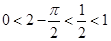 ,则
,则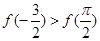 ,故选A.
,故选A.
考点:函数的奇偶性、单调性、周期性.

练习册系列答案
相关题目
设函数 .若
.若 ,则( )
,则( )
A. | B. |
C. | D. |
设函数
 ,集合
,集合 其中
其中
 <
< ,则使
,则使 成立的实数对
成立的实数对 有( )
有( )
| A.0个 | B.1个 | C.2个 | D.无数多个 |
函数 的单调递减区间为( )
的单调递减区间为( )
| A.(-∞,-3) | B.(-∞,-1) | C.(1,+∞) | D.(-3,-1) |
函数 的零点个数为( )
的零点个数为( )
| A.1 | B.2 | C.3 | D.4 |
实数x,y满足 ,若函数z=x+y的最大值为4,则实数a的值为( )
,若函数z=x+y的最大值为4,则实数a的值为( )
| A.2 | B.3 | C. | D.4 |
已知定义在 上的函数
上的函数 满足
满足 为奇函数,函数
为奇函数,函数 关于直线
关于直线 对称,则下列式子一定成立的是( )
对称,则下列式子一定成立的是( )
A. | B. |
C. | D.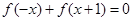 |
已知函数 (a为常数).若
(a为常数).若 在区间[-1,+∞)上是增函数,则a的取值范围是( )
在区间[-1,+∞)上是增函数,则a的取值范围是( )
A.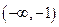 |
B.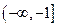 |
C.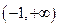 |
D. |
 acosC,则sinA+sinB的最大值是( )
acosC,则sinA+sinB的最大值是( )