题目内容
设函数
 ,集合
,集合 其中
其中
 <
< ,则使
,则使 成立的实数对
成立的实数对 有( )
有( )
| A.0个 | B.1个 | C.2个 | D.无数多个 |
A
解析试题分析:首先研究函数 的性质知,
的性质知, 是奇函数,在实数集
是奇函数,在实数集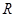 上是减函数,当
上是减函数,当 时,
时, ,当
,当 时,
时, ,若
,若 存在,则
存在,则 ,即
,即 ,此方程组除
,此方程组除 外无其他实数解,故符合题意的实数对
外无其他实数解,故符合题意的实数对 不存在.选A.
不存在.选A.
考点:函数的性质,方程组的解.

练习册系列答案
 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
已知函数
 ,数列
,数列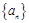 满足
满足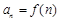
 ,且数列
,且数列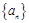 是递增数列,则实数
是递增数列,则实数 的取值范围是 ( )
的取值范围是 ( )
A. | B. | C. | D. |
已知函数 和
和 都是定义在R上的偶函数,若
都是定义在R上的偶函数,若 时,
时, ,则
,则 为( )
为( )
| A.正数 | B.负数 | C.零 | D.不能确定 |
若函数 满足
满足 且
且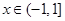 时,
时,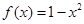 ,函数
,函数 分别在两相邻对称轴
分别在两相邻对称轴 与
与 处取得最值1与-1,则函数
处取得最值1与-1,则函数 在区间
在区间 内零点的个数为( )
内零点的个数为( )
| A.1006 | B.1007 | C.1008 | D.1010 |
定义域为 的函数
的函数 满足
满足 ,当
,当 时,
时, 若当
若当 时,函数
时,函数 恒成立,则实数
恒成立,则实数 的取值范围为( )
的取值范围为( )
A. | B.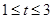 | C. | D. |
已知函数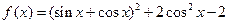 ,则
,则 函数图象的一条对称轴方程是( )
函数图象的一条对称轴方程是( )
A. |
B. |
C.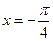 |
D. |
函数 的图象向右平移1个单位长度,所得图象与曲线
的图象向右平移1个单位长度,所得图象与曲线 关于y轴对称,则
关于y轴对称,则 ( )
( )
A. |
B. |
C. |
D. |
 的定义域为实数集
的定义域为实数集 ,
, 对于任意的
对于任意的 都有
都有 .若在区间
.若在区间 上函数
上函数 恰有四个不同的零点,则实数
恰有四个不同的零点,则实数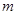 的取值范围是( ).
的取值范围是( ).




 (其中
(其中 ),若
),若 的图象如下图(左)所示,则
的图象如下图(左)所示,则 的图象是 ( )
的图象是 ( )

