题目内容
函数
的单调递减区间为（ ）
| A．（－∞，－3） | B．（－∞，－1） | C．(1，+∞) | D．(－3，－1) |
A
解析试题分析：由
，得
或
，∴
的定义域为
．可看作由
和
复合而成的，＝
在
上递减，在
上递增，又在定义域内单调递增，∴在上递减，在上递增，所以的单调递减区间是，故选A．
考点：复合函数的单调性．
练习册系列答案
阅读快车系列答案
相关题目
(其中
)，若
的图象如下图（左）所示，则
的图象是 ( )
设函数
，则
是（）
| A．最小正周期为p的奇函数 | B．最小正周期为p的偶函数 |
C．最小正周期为 的奇函数 | D．最小正周期为的偶函数 |
已知函数
和
都是定义在R上的偶函数，若
时，
，则
为（ ）
| A．正数 | B．负数 | C．零 | D．不能确定 |
下列函数，在其定义域内既是奇函数又是增函数的是 ( )
A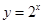．  | B．  |
C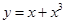． | D．  |
函数
的定义域是（ ）
A． | B． | C． | D． |
设函数
，对任意
恒成立，则实数m的取值范围是( )
A． |
B． |
C． |
D． |
函数
的定义域为R，
，对任意
，则
的解集为（ ）
A． |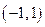
B． |
C． |
| D．R |
函数f(x)=tan(2x-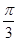
)的单调递增区间是（）
A．[ , ](k∈Z) |
| B．（,）(k∈Z) |
C．[ , ](k∈Z) |
D．（ ， ）(k∈Z) |