题目内容
【题目】甲、乙两位同学参加诗词大会，设甲、乙两人每道题答对的概率分别为
和
.假定甲、乙两位同学答题情况互不影响，且每人各次答题情况相互独立.
（1）用
表示甲同学连续三次答题中答对的次数，求随机变量的分布列和数学期望；
（2）设
为事件“甲、乙两人分别连续答题三次，甲同学答对的次数比乙同学答对的次数恰好多2”，求事件发生的概率.
【答案】（1）分布列见解析，
；（2）
.
【解析】
（1）先由题意，得到
服从二项分布，以及的所有可能的取值，求出对应的概率，即可得出分布列与数学期望；
（2）先设
为乙连续3次答题中答对的次数，由题意得到服从二项分布，根据二项分布的概率计算公式，即可求出结果.
（1）由题意知
，
的所有可能的取值为0，1，2，3，
；
；
；
，
所以的分布列为
| 0 | 1 | 2 | 3 |
|
|
|
|
|
数学期望
.
（或
.）
（2）设为乙连续3次答题中答对的次数，
由题意知
，
，
，
所以
（
且
）
（
且
）
.
练习册系列答案
相关题目
【题目】某家庭为了解冬季用电量
（度）与气温
之间的关系，随机统计了某5天的用电量与当天气温，并制作了对照表，经过统计分析，发现气温在一定范围内时，用电量与气温具有线性相关关系：
| 0 | 1 | 2 | 3 | 4 |
| 15 | 12 | 11 | 9 | 8 |
（1）求出用电量关于气温
的线性回归方程；
（2）在这5天中随机抽取两天，求至少有一天用电量低于10（度）的概率.
（附：回归直线方程的斜率和截距的最小二乘法估计公式为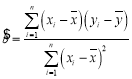
，
）
