题目内容
【题目】假定一个弹珠（设为质点
，半径忽略不计）的运行轨迹是以小球（半径
）的中心
为右焦点的椭圆
，已知椭圆的右端点
到小球表面最近的距离是1，椭圆的左端点
到小球表面最近的距离是5.
.
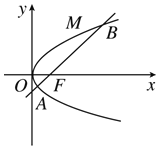
（1）求如图给定的坐标系下椭圆的标准方程；
（2）弹珠由点开始绕椭圆轨道逆时针运行，第一次与轨道中心
的距离是
时，弹珠由于外力作用发生变轨，变轨后的轨道是一条直线，称该直线的斜率
为“变轨系数”，求的取值范围，使弹珠和小球不会发生碰撞.
【答案】（1）
；（2）
.
【解析】
（1）根据题意可得
，从而可求椭圆
的标准方程；
（2）根据与轨道中心
的距离是
可以求出点
的坐标，进而设出直线方程，利用直线与圆相离可求
的取值范围.
（1）由题意，
：；
（2）设
，联立与
，可求出
，
设直线方程为
，即
，
弹珠和小球不会发生碰撞，说明圆心
到直线的距离大于圆半径1，
所以
，解得.
练习册系列答案
阅读快车系列答案
相关题目
