题目内容
如图,圆柱的高为2,底面半径为3,AE、DF是圆柱的两条母线,B、C是下底面圆周上的两点,已知四边形ABCD是正方形.
(1)求证: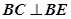 ;
;
(2)求正方形ABCD的边长;
(3)求直线 与平面
与平面 所成角的正弦值.
所成角的正弦值.
(1)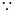 AE是圆柱的母线
AE是圆柱的母线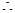
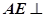 底面BEFC, 又
底面BEFC, 又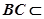 面BEFC
面BEFC 
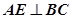
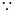 又
又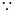 ABCD是正方形
ABCD是正方形 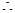
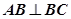 又
又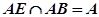
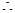
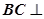 面ABE
面ABE
又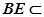 面ABE
面ABE 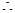
 …… 3分
…… 3分
(2) 四边形
四边形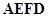 为矩形,且ABCD是正方形
为矩形,且ABCD是正方形 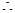 EF
EF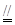 BC
BC 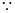
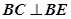
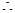 四边形EFBC为矩形
四边形EFBC为矩形 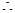 BF为圆柱下底面的直径 …… 4分
BF为圆柱下底面的直径 …… 4分
设正方形ABCD的边长为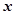 ,则AD=EF=AB=
,则AD=EF=AB=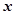
在直角 中AE=2,AB=
中AE=2,AB=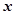 ,且BE2+AE
,且BE2+AE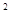 = AB
= AB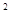 ,得BE
,得BE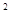 =
=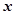 2-4
2-4
在直角 中BF=6,EF=
中BF=6,EF=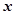 ,且BE
,且BE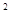 +EF
+EF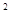 = BF
= BF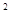 ,的BE2=36-
,的BE2=36-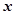 2 …… 6分
2 …… 6分
解得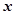 =
=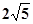 ,即正方形ABCD的边长为
,即正方形ABCD的边长为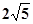 …… 7分
…… 7分
(3)如图以F为原点建立空间直角坐标系,则A( ,0,2),B(
,0,2),B( ,4,0),
,4,0),
E( ,0,0),
,0,0), (
( ,0, 2),
,0, 2),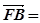 (
( ,4,0),
,4,0), 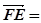 (
(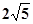 ,0,0)
,0,0)
设面AEF的法向量为 (
(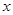 ,
,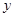 ,
,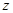 ),则
),则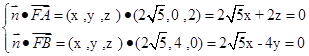
令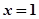 ,则
,则 即
即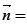 (
(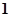 ,
,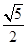 ,-
,-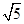 ) …… 11分
) …… 11分
设直线 与平面
与平面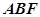 所成角的大小为
所成角的大小为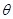 ,则
,则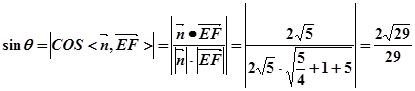 …… 12分
…… 12分
所以直线 与平面
与平面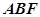 所成角的正弦值为
所成角的正弦值为 解析
解析

练习册系列答案
相关题目
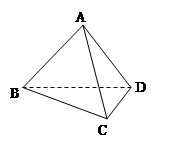
如图,三棱柱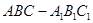 的各棱长均为2,侧棱
的各棱长均为2,侧棱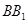 与底面
与底面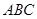 所成的角为
所成的角为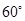 ,
,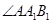 为锐角,且侧面
为锐角,且侧面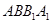 ⊥底面
⊥底面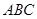 ,给出下列四个结论:
,给出下列四个结论: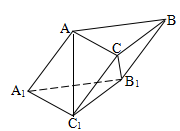
①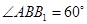 ;
;
②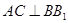 ;
;
③直线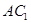 与平面
与平面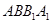 所成的角为
所成的角为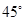 ;
;
④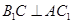 .
.
其中正确的结论是( )
| A.①③ | B.②④ | C.①③④ | D.①②③④ |
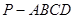 的侧面
的侧面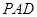 垂直于底面
垂直于底面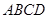 ,
,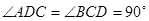 ,
,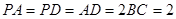 ,
,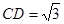 ,
,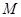 在棱
在棱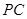 上,
上,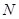 是
是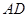 的中点,二面角
的中点,二面角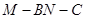 为
为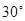
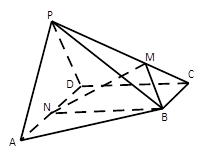
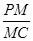 的值;
的值; 与平面
与平面 所成角的正弦值.
所成角的正弦值. ,
, ,
, 
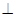 底面ABCD,E是PC的中点。
底面ABCD,E是PC的中点。
 中,底面
中,底面 是矩形,
是矩形,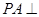 平面
平面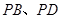 与平面
与平面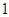 和
和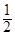 ,
,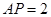 ,
,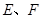 依次是
依次是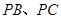 的中点.
的中点.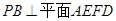 ;
;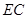 与平面
与平面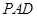 所成角的正弦值.
所成角的正弦值.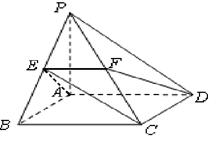
 为正三角形,
为正三角形,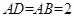 ,
,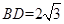 ,AC与BD交于O点.将
,AC与BD交于O点.将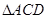 沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为
沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为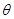 ,且P点在平面ABCD内的射影落在
,且P点在平面ABCD内的射影落在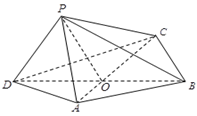
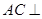 平面PBD;
平面PBD;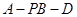 的余弦值为
的余弦值为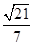 ,求
,求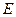 ,
,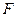 分别是直角三角形
分别是直角三角形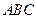 边
边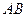 和
和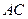 的中点,
的中点,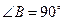 ,沿
,沿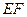 将三角形
将三角形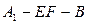 ,若
,若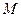 为线段
为线段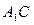 中点.求证:
中点.求证: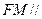 平面
平面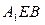 ;
;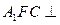 平面
平面 .
.


 中,侧棱
中,侧棱 ,底面
,底面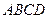 是直角梯形,
是直角梯形,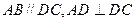 ,且
,且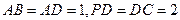 ,
,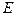 是
是 的中点.
的中点.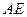 与
与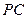 所成的角;
所成的角;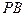 上是否存在一点
上是否存在一点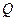 ,使得
,使得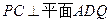 ?若存在,求出
?若存在,求出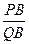 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.