题目内容
5．棱长为2的正方体被一平面截得的几何体的三视图如图所示，那么被截去的几何体的体积是（ ）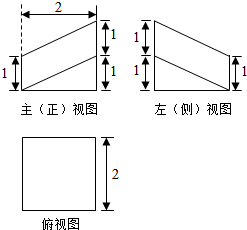
| A． | $\frac{14}{3}$ | B． | $\frac{10}{3}$ | C． | 4 | D． | $\frac{16}{3}$ |
分析 根据几何体的三视图，得出该几何体是棱长为2的正方体的一部分，由此求出该几何体的体积．
解答 
解：根据几何体的三视图，得；
该几何体是棱长为2的正方体被平面分成体积相等的两部分中的一部分，
如图所示；
所以该几何体的体积为$\frac{1}{2}$×23=4．
故选：C．
点评 本题考查了空间几何体的三视图的应用问题，解题的关键根据三视图得出几何体的结构特征是什么．
练习册系列答案
相关题目
15．已知过点A（1，m）恰能作曲线f（x）=x3-3x的两条切线，则m的值是（ ）
| A． | -1 | B． | -2 | C． | -3 | D． | -3或-2 |
13．定义在R上的偶函数f（x）满足f（x+1）=-f（x），且在[-5，-4]上是减函数，α、β是锐角三角形的两个内角，则（ ）
| A． | f（sinα）＞f（cosβ） | B． | f（sinα）＞f（sinβ） | C． | f（sinα）＜f（cosβ） | D． | f（cosα）＞f（cosβ） |
17．已知变量x、y满足约束条件：$\left\{\begin{array}{l}{y≥x}\\{x+2y≤2}\\{x≥-2}\end{array}\right.$，则z=x-3y的最小值是（ ）
| A． | -$\frac{4}{3}$ | B． | 4 | C． | -4 | D． | -8 |
14．在一项吃零食与性别的调查中，运用2×2列联表进行独立性检验得到K2≈2.521，那么判断吃零食和性别有关的这种判断的出错率为（ ）
| A． | 1% | B． | 99% | C． | 15% | D． | 90% |