题目内容
已知函数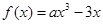 .
.
(1)当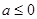 时,求函数
时,求函数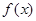 单调区间;
单调区间;
(2)若函数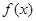 在区间[1,2]上的最小值为
在区间[1,2]上的最小值为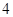 ,求
,求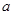 的值.
的值.
(1)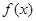 在
在 上是增函数 (2)
上是增函数 (2)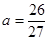
解析试题分析:
(1)对函数求导,求导函数大于0和小于0的解集,该函数的导函数为二次函数,且含有参数,可以通过判断该二次函数的图像的开口零点个数等确定导函数大于0和小于0的解集,进而得到单调区间.
(2)通过(1)可以得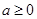 时,函数在区间[1,2]的单调性得到最大值求出8(并判断是否符合
时,函数在区间[1,2]的单调性得到最大值求出8(并判断是否符合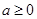 ),a<0时,继续通过讨论f(x)的导函数,通过对导函数(为二次函数)的开口 根的个数 根的大小与是否在区间[1,3]来确定原函数在区间[1,2]上的最值,进而得到a的值.
),a<0时,继续通过讨论f(x)的导函数,通过对导函数(为二次函数)的开口 根的个数 根的大小与是否在区间[1,3]来确定原函数在区间[1,2]上的最值,进而得到a的值.
试题解析:
(1)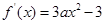 1分
1分
因为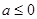 ,所以
,所以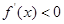 对任意实数
对任意实数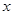 恒成立,
恒成立,
所以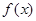 在
在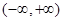 是减函数 4分
是减函数 4分
(2)当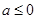 时,由(1)可知,
时,由(1)可知,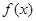 在区间[1,2]是减函数
在区间[1,2]是减函数
由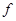
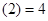 得
得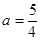 ,(不符合舍去) 6分
,(不符合舍去) 6分
当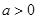 时,
时,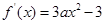
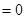 的两根
的两根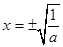 7分
7分
①当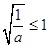 ,即
,即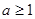 时,
时,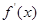
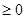 在区间[1,2]恒成立,
在区间[1,2]恒成立,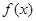 在区间[1,2]是增函数,由
在区间[1,2]是增函数,由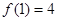
得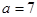 9分
9分
②当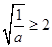 ,即
,即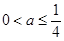 时
时 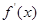
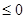 在区间[1,2]恒成立
在区间[1,2]恒成立 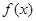 在区间[1,2]是减函数
在区间[1,2]是减函数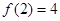 ,
,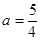 (不符合舍去) 11分
(不符合舍去) 11分
③当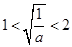 ,即
,即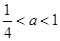 时,
时,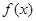 在区间
在区间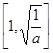 是减函数,
是减函数,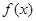 在区间
在区间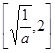 是增函数;所以
是增函数;所以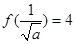 无解 13分
无解 13分
综上,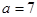 14分
14分
考点:导数 最值 单调性 二次函数

练习册系列答案
相关题目
 ,
,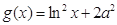 ,其中
,其中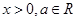 .
.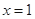 是函数
是函数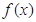 的极值点,求
的极值点,求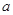 的值;
的值;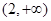 上单调递增,求
上单调递增,求 的取值范围;
的取值范围;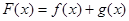 ,求证:
,求证: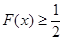 .
.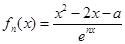 ,其中
,其中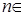 N*,a
N*,a R,e是自然对数的底数.
R,e是自然对数的底数. 的零点;
的零点;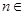 N*,
N*,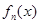 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围; 在R上是单调函数,探究函数
在R上是单调函数,探究函数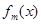 的单调性.
的单调性. .
.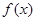 的最大值;
的最大值;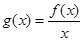 ,证明:
,证明: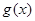 有最大值
有最大值 ,且
,且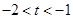 .
.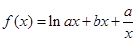 (
( 、
、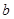 为常数),在
为常数),在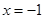 时取得极值.
时取得极值.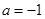 时,关于
时,关于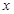 的方程
的方程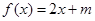 有两个不相等的实数根,求实数
有两个不相等的实数根,求实数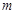 的取值范围;
的取值范围;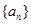 满足
满足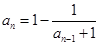 (
(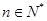 且
且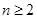 ),
),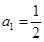 ,数列
,数列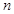 项和为
项和为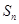 ,
,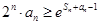 (
(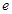 是自然对数的底).
是自然对数的底).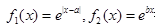
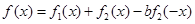 ,是否存在a,b
,是否存在a,b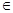 R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;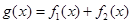 在R上的单调区间;
在R上的单调区间;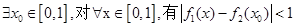 成立.求a的取值范围.
成立.求a的取值范围. >0.
>0.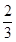 x+
x+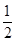 ,h(x)=
,h(x)=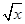 ,设F(x)=f(x)-h(x),求F(x)的单调区间与极值.
,设F(x)=f(x)-h(x),求F(x)的单调区间与极值.