题目内容
7. 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E是PD的中点.
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E是PD的中点.(1)证明:PB∥平面AEC;
(2)设$AP=1,AD=\sqrt{3}$,三棱锥P-ABD的体积$V=\frac{{\sqrt{3}}}{4}$,求AC与平面PBC所成角的正弦值.
分析 (1)设BD和AC交于点O,连接EO,由中位线定理和线面平行的判定定理,即可得证;
(2)运用棱锥的条件公式,计算可得AB,AC,作AH⊥PB交PB于H,在直角三角形PAB中,运用面积求得AH,由线面垂直的性质和判定,可得AH垂直于平面PBC,由线面角的定义,可得AC与平面PBC所成角的平面角为∠ACH,再由解直角三角形的知识,即可得到所求正弦.
解答 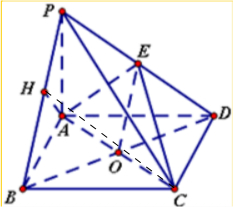 解:(1)设BD和AC交于点O,连接EO,
解:(1)设BD和AC交于点O,连接EO,
因为ABCD为矩形,所以O为BD的中点,又E为PD的中点,
所以EO∥PB,且EO在平面AEC内,PB不在平面AEC内,
所以PB∥平面AEC;
(2)由$AP=1,AD=\sqrt{3}$,
$V=\frac{1}{6}PA•AB•AD=\frac{{\sqrt{3}}}{4}$,得$AB=\frac{3}{2}$,
AC=$\sqrt{3+\frac{9}{4}}$=$\frac{\sqrt{21}}{2}$,
作AH⊥PB交PB于H,
由BC⊥PA,BC⊥AB,
即有BC⊥面PAB,所以BC⊥AH,
所以AH⊥平面PBC,
故$AH=\frac{PA•AB}{PB}=\frac{{3\sqrt{13}}}{13}$,
故AC与平面PBC所成角的平面角为∠ACH,
则$sin∠ACH=\frac{AH}{AC}=\frac{{2\sqrt{273}}}{91}$.
点评 本题考查空间直线和平面的位置关系:平行和垂直,同时考查直线和平面所成的角的求法,考查运算能力,属于中档题.

练习册系列答案
相关题目
18.把函数y=sin(5x-$\frac{π}{2}$)的图象向右平移$\frac{π}{4}$个单位长度,再把所得图象上各点的横坐标缩短为原来的$\frac{1}{2}$,纵坐标不变,所得图象对应的函数解析式为( )
| A. | y=sin(10x-$\frac{3}{4}$π) | B. | y=sin(10x-$\frac{7}{2}$π) | C. | y=sin(10x-$\frac{3}{2}$x) | D. | y=sin(10x-$\frac{7}{4}$π) |
19.在△ABC中,若acosB=bcosA,则△ABC是( )
| A. | 直角三角形 | B. | 等腰三角形 | ||
| C. | 等边三角形 | D. | 等腰或直角三角形 |
17.下列描述不是解决问题的算法的是( )
| A. | 从中山到北京先坐汽车,再坐火车 | |
| B. | 解一元一次方程的步骤是去分母、去括号、移项、合并同类项、化系数为1 | |
| C. | 方程x2-4x+3=0有两个不等的实根 | |
| D. | 解不等式ax+3>0时,第一步移项,第二步讨论 |