题目内容
【题目】已知二次函数f（x）满足f（x）=f（2-x），且f（1）=6，f（3）=2．若不等式f（x）＞2mx+1在[-1，3]恒成立，则实数m的取值范围是______．
【答案】（-
）
【解析】
根据f（x）=f（2-x），且f（1）=6，f（3）=2．求解f（x）的解析式，带入不等式，讨论对称轴与区间端点大小，即可求解实数m的取值范围．
由题意，设f（x）=ax2+bx+c，
由f（x）=f（2-x），可得
，即b=-2a；
且f（1）=6，f（3）=2．
可得
，
解得：c=5，a=-1，b=2
∴f（x）=-x2+2x+5，
则-x2+2x+5＞2mx+1在[-1，3]恒成立，
令h（x）=x2+（2m-2）x-4＜0．
根据二次函数的性质，可得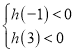
，即
得
．
故答案为：（-）．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
