题目内容
设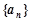 是有穷数列,且项数
是有穷数列,且项数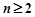 .定义一个变换
.定义一个变换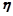 :将数列
:将数列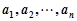 ,变成
,变成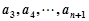 ,其中
,其中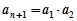 是变换所产生的一项.从数列
是变换所产生的一项.从数列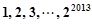 开始,反复实施变换
开始,反复实施变换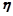 ,直到只剩下一项而不能变换为止.则变换所产生的所有项的乘积为
,直到只剩下一项而不能变换为止.则变换所产生的所有项的乘积为
A.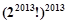 | B.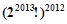 | C.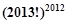 | D.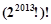 |
A
解析试题分析::数列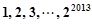 共有
共有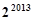 项,它们的乘积为
项,它们的乘积为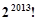 .经过
.经过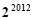 次变换,产生了有
次变换,产生了有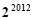 项的一个新数列,它们的乘积也为
项的一个新数列,它们的乘积也为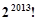 .对新数列进行同样的变换,直至最后只剩下一个数,它也是
.对新数列进行同样的变换,直至最后只剩下一个数,它也是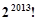 ,变换终止.在变换过程中产生的所有的项,可分为2013组,每组的项数依次为
,变换终止.在变换过程中产生的所有的项,可分为2013组,每组的项数依次为 ,乘积均为
,乘积均为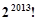 ,故答案为A
,故答案为A
考点:数列的求和
点评:解决的关键是利用数列的特点进行求解积,得到结论,属于基础题。

练习册系列答案
相关题目
已知数列 的通项公式为
的通项公式为
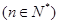 ,其前n项和为
,其前n项和为 ,则在数列
,则在数列 中,有理数项的项数为( )
中,有理数项的项数为( )
| A.42 | B.43 | C.44 | D.45 |
已知数列 满足
满足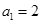 ,
,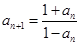 (
( N*),则连乘积
N*),则连乘积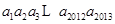 的值为( )
的值为( )
A.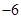 | B.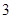 | C.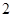 | D.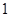 |
已知数列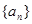 满足
满足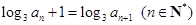 ,且
,且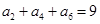 ,则
,则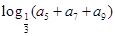 的值是( )
的值是( )
A.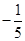 | B.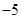 | C.5 | D.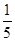 |
数列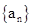 的通项公式为
的通项公式为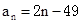 ,当该数列的前
,当该数列的前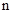 项和
项和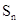 达到最小时,
达到最小时,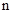 等于( )
等于( )
A.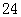 | B.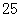 | C.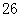 | D.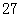 |
设等比数列 的公比为
的公比为 ,前n项和为
,前n项和为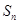 ,若
,若 ,
,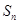 ,
,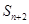 成等差数列,则公比
成等差数列,则公比 为( ).
为( ).
A.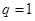 | B. | C. 或 或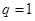 | D. 或 或 |
数列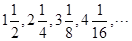 前n项的和为()
前n项的和为()
A.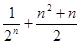 | B.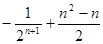 |
C.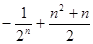 | D.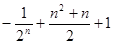 |
 为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为
为n个正数a1+a2+…+an的“均倒数”已知数列{an}的各项均为正,且其前n项的“均倒数”为 则数列{an}的通项公式为
则数列{an}的通项公式为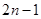
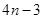
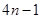

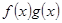 =ax,且f′(x)g(x)+f(x)·g′(x)<0,
=ax,且f′(x)g(x)+f(x)·g′(x)<0,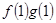 +
+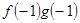 =
=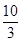 ,若有穷数列{
,若有穷数列{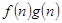 }(n∈N*)的前n项和等于
}(n∈N*)的前n项和等于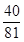 ,则n等于 .
,则n等于 .