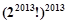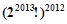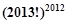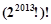题目内容
已知数列 的通项公式为
的通项公式为
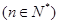 ,其前n项和为
,其前n项和为 ,则在数列
,则在数列 中,有理数项的项数为( )
中,有理数项的项数为( )
| A.42 | B.43 | C.44 | D.45 |
B
解析试题分析: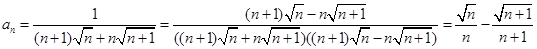 ,
,
∴ 为有理项,∴
为有理项,∴ 且
且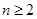 ,∴有理数项的项数为43项.
,∴有理数项的项数为43项.
考点:1.分母有理化;2.裂项相消法求和;3.数列的通项公式.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
数列 的通项公式为
的通项公式为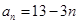 ,
,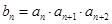 ,
, 是数列
是数列 的前
的前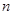 项和,则
项和,则 的最大值为( )
的最大值为( )
| A.280 | B.300 | C.310 | D.320 |
数列1,1+2,1+2+4,…,1+2+22+…+2n-1,…的前n项和Sn>1020,那么n的最小值是( )
| A.7 | B.8 | C.9 | D.10 |
数列{an}中,an+1+(-1)nan=2n-1,则数列{an}的前12项和等于( )
| A.76 | B.78 |
| C.80 | D.82 |
数列{an}的通项公式an= ,若{an}前n项和为24,则n为( ).
,若{an}前n项和为24,则n为( ).
| A.25 | B.576 | C.624 | D.625 |
 作直线
作直线 交曲线
交曲线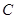 :
: (
(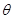 为参数)于
为参数)于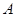 、
、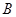 两点,若
两点,若 成等比数列,求直线
成等比数列,求直线 是由正数组成的等比数列,
是由正数组成的等比数列, 表示
表示 项的和,若
项的和,若 ,
, ,则
,则 的值是 ( )
的值是 ( )
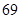
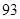

 表示位于从上到下第
表示位于从上到下第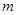 行,从左到右
行,从左到右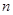 列的数,比如
列的数,比如 ,若
,若 ,则有( )
,则有( )

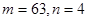
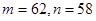
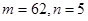
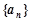 是有穷数列,且项数
是有穷数列,且项数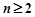 .定义一个变换
.定义一个变换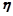 :将数列
:将数列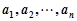 ,变成
,变成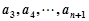 ,其中
,其中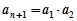 是变换所产生的一项.从数列
是变换所产生的一项.从数列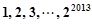 开始,反复实施变换
开始,反复实施变换