题目内容
【题目】已知椭圆
： 
经过点
，且离心率为
．
（I）求椭圆
的方程；
（II）若一组斜率为
的平行线，当它们与椭圆
相交时，证明：这组平行线被椭圆
截得的线段的中点在同一条直线上．
【答案】(Ⅰ) 
(Ⅱ)见解析
【解析】试题分析：(Ⅰ)由
经过点
，可得
，根据离心率为
，结合
可得
，从而可得椭圆
的方程；(Ⅱ) 设直线与椭圆的两个交点坐标分别为
， 
，它们的中点坐标为
．由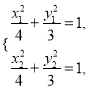
，两式相减，结合
， 
， 
，化简可得
，所以这组平行线被椭圆
截得的线段的中点在同一条直线上.
试题解析：(Ⅰ)由已知可得
， 
， 又
，可得
， 
， 所以椭圆
的方程为
．
(Ⅱ) 证明：设直线与椭圆的两个交点坐标分别为
， 
，它们的中点坐标为
．由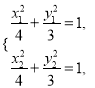
两式相减可得
， 
，由已知
，所以
，故直线被椭圆
截得的线段的中点都在直线
上.
练习册系列答案
相关题目
