题目内容
函数 的单调递减区间为( )
的单调递减区间为( )
A.( 1,1) 1,1) | B.(0,1] | C.[1,+∞) | D.( ∞,-1)∪(0,1] ∞,-1)∪(0,1] |
B
解析试题分析:因为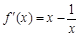 ,所以由
,所以由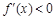 得
得 .又因为
.又因为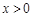 ,所以
,所以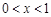 .所求函数的单调递减区间为(0,1].
.所求函数的单调递减区间为(0,1].
考点:由导数求函数单调性

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数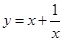 的导数是( )
的导数是( )
A.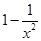 | B.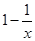 | C.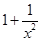 | D.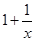 |
设函数 是
是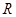 上以5为周期的可导偶函数,则曲线
上以5为周期的可导偶函数,则曲线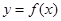 在
在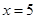 处的切线的斜率为
处的切线的斜率为
A.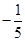 | B.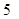 | C.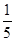 | D. |
已知函数 的导函数存在,则函数
的导函数存在,则函数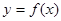 在一点的导数值为
在一点的导数值为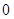 是函数
是函数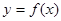 在这点取极值的( )
在这点取极值的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
函数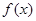 的定义域为开区间
的定义域为开区间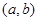 ,导函数
,导函数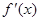 在
在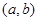 内的图像如图所示,则函数
内的图像如图所示,则函数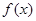 在开区间
在开区间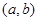 内有极小值点( )
内有极小值点( )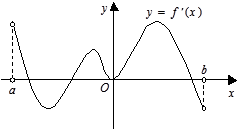
| A.1个 | B.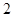 个 个 | C.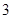 个 个 | D.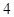 个 个 |
已知函数f(x)=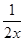 -cosx,若
-cosx,若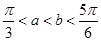 ,则( )
,则( )
| A.f(a)>f(b) | B.f(a)<f(b) | C.f(a)=f(b) | D.f(a)f(b)>0 |
已知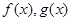 都是定义在R上的函数,
都是定义在R上的函数,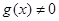 ,
,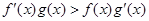 ,且
,且
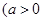 ,且
,且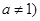 ,
,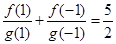 .若数列
.若数列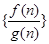 的前n项和大于62,则n的最小值为( )
的前n项和大于62,则n的最小值为( )
| A.6 | B.7 | C.8 | D.9 |
若函数f(x)=ax4+bx2+c满足f′(1)=2,则f′(-1)等于( )
| A.-1 | B.- 2 | C.2 | D.0 |
已知函数f(x)的导函数为f′(x),且满足f(x)=2xf′(e)+ln x,则f′(e)=( )
| A.1 | B.-1 | C.-e-1 | D.-e |