题目内容
若函数f(x)=ax4+bx2+c满足f′(1)=2,则f′(-1)等于( )
| A.-1 | B.- 2 | C.2 | D.0 |
B
解析

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
若函数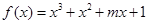 是R上的单调函数,则实数m的取值范围是( )
是R上的单调函数,则实数m的取值范围是( )
A.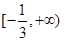 | B.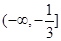 | C.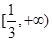 | D.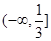  |
函数 的单调递减区间为( )
的单调递减区间为( )
A.( 1,1) 1,1) | B.(0,1] | C.[1,+∞) | D.( ∞,-1)∪(0,1] ∞,-1)∪(0,1] |
设底为等边三角形的直棱柱的体积为V,那么其表面积最小时,底面边
长为( )
A.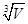 | B.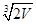 | C.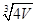 | D.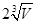 |
已知直线y=x+1与曲线y=ln(x+a)相切,则a的值为 ( ).
| A.1 | B.2 | C.-1 | D.-2 |
函数y=1+3x-x3有 ( ).
| A.极小值-1,极大值1 | B.极小值-2,极大值3 |
| C.极小值-2,极大值2 | D.极小值-1,极大值3 |
曲线y=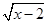 在点P(3,1)处的切线斜率为 ( ).
在点P(3,1)处的切线斜率为 ( ).
A.-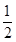 | B.0 | C.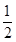 | D.1 |
函数y=(3-x2)ex的单调递增区间是( )
| A.(-∞,0) |
| B.(0,+∞) |
| C.(-∞,-3)和(1,+∞) |
| D.(-3,1) |
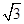 ),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )
),那么曲线y=f(x)上任一点的切线的倾斜角α的取值范围是( )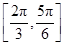
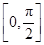 ∪
∪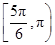
 ∪
∪